Question-122927

Question Number 122927 by bemath last updated on 21/Nov/20

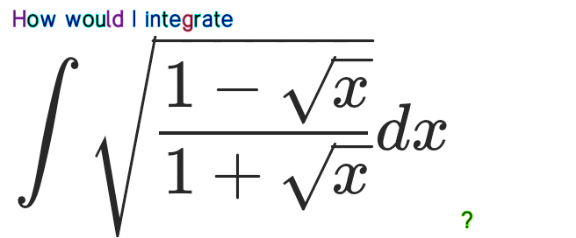
Commented by liberty last updated on 21/Nov/20

μ(x)=∫ (√((1−(√x))/(1+(√x)))) dx [ let (√x) = sin z ⇒ dx = sin 2z dz ] μ(x)=∫ (√((1−sin z)/(1+sin z))) (sin 2z dz ) μ(x)=∫ ((√((1−sin z)^2 ))/(cos z)) (2sin z cos z ) dz μ(x)= ∫ 2sin z(1−sin z) dz μ(x)=∫(2sin z−2((1/2)−cos 2z))dz μ(x)=−2cos z−z+sin 2z + c μ(x)=2cos z(sin z−1)−z + c μ(x)=2(√(1−x)) ((√x) −1)−sin^(−1) (√x) + c

$$\mu\left({x}\right)=\int\:\sqrt{\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}+\sqrt{{x}}}}\:{dx}\: \\ $$$$\:\left[\:{let}\:\sqrt{{x}}\:=\:\mathrm{sin}\:{z}\:\Rightarrow\:{dx}\:=\:\mathrm{sin}\:\mathrm{2}{z}\:{dz}\:\right] \\ $$$$\mu\left({x}\right)=\int\:\sqrt{\frac{\mathrm{1}−\mathrm{sin}\:{z}}{\mathrm{1}+\mathrm{sin}\:{z}}}\:\left(\mathrm{sin}\:\mathrm{2}{z}\:{dz}\:\right)\: \\ $$$$\mu\left({x}\right)=\int\:\frac{\sqrt{\left(\mathrm{1}−\mathrm{sin}\:{z}\right)^{\mathrm{2}} }}{\mathrm{cos}\:{z}}\:\left(\mathrm{2sin}\:{z}\:\mathrm{cos}\:{z}\:\right)\:{dz} \\ $$$$\mu\left({x}\right)=\:\int\:\mathrm{2sin}\:{z}\left(\mathrm{1}−\mathrm{sin}\:{z}\right)\:{dz}\: \\ $$$$\mu\left({x}\right)=\int\left(\mathrm{2sin}\:{z}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{cos}\:\mathrm{2}{z}\right)\right){dz} \\ $$$$\mu\left({x}\right)=−\mathrm{2cos}\:{z}−{z}+\mathrm{sin}\:\mathrm{2}{z}\:+\:{c} \\ $$$$\mu\left({x}\right)=\mathrm{2cos}\:{z}\left(\mathrm{sin}\:{z}−\mathrm{1}\right)−{z}\:+\:{c} \\ $$$$\mu\left({x}\right)=\mathrm{2}\sqrt{\mathrm{1}−{x}}\:\left(\sqrt{{x}}\:−\mathrm{1}\right)−\mathrm{sin}^{−\mathrm{1}} \sqrt{{x}}\:+\:{c} \\ $$

Answered by MJS_new last updated on 21/Nov/20

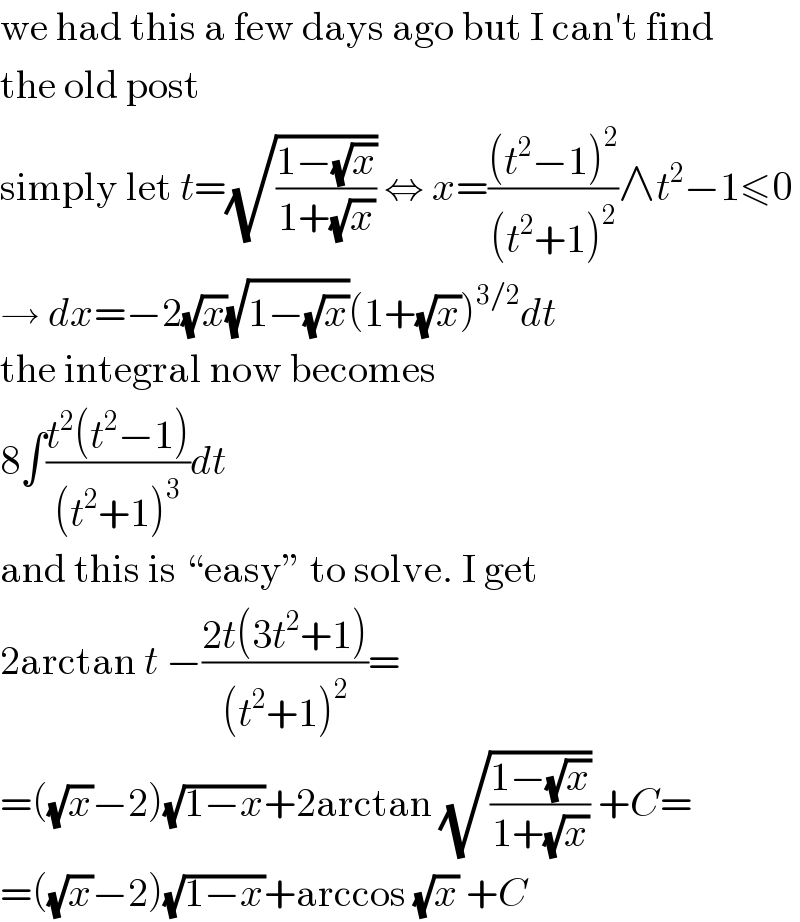
we had this a few days ago but I can′t find the old post simply let t=(√((1−(√x))/(1+(√x)))) ⇔ x=(((t^2 −1)^2 )/((t^2 +1)^2 ))∧t^2 −1≤0 → dx=−2(√x)(√(1−(√x)))(1+(√x))^(3/2) dt the integral now becomes 8∫((t^2 (t^2 −1))/((t^2 +1)^3 ))dt and this is “easy” to solve. I get 2arctan t −((2t(3t^2 +1))/((t^2 +1)^2 ))= =((√x)−2)(√(1−x))+2arctan (√((1−(√x))/(1+(√x)))) +C= =((√x)−2)(√(1−x))+arccos (√x) +C

$$\mathrm{we}\:\mathrm{had}\:\mathrm{this}\:\mathrm{a}\:\mathrm{few}\:\mathrm{days}\:\mathrm{ago}\:\mathrm{but}\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{find} \\ $$$$\mathrm{the}\:\mathrm{old}\:\mathrm{post} \\ $$$$\mathrm{simply}\:\mathrm{let}\:{t}=\sqrt{\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}+\sqrt{{x}}}}\:\Leftrightarrow\:{x}=\frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\wedge{t}^{\mathrm{2}} −\mathrm{1}\leqslant\mathrm{0} \\ $$$$\rightarrow\:{dx}=−\mathrm{2}\sqrt{{x}}\sqrt{\mathrm{1}−\sqrt{{x}}}\left(\mathrm{1}+\sqrt{{x}}\right)^{\mathrm{3}/\mathrm{2}} {dt} \\ $$$$\mathrm{the}\:\mathrm{integral}\:\mathrm{now}\:\mathrm{becomes} \\ $$$$\mathrm{8}\int\frac{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dt} \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:“\mathrm{easy}''\:\mathrm{to}\:\mathrm{solve}.\:\mathrm{I}\:\mathrm{get} \\ $$$$\mathrm{2arctan}\:{t}\:−\frac{\mathrm{2}{t}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=\left(\sqrt{{x}}−\mathrm{2}\right)\sqrt{\mathrm{1}−{x}}+\mathrm{2arctan}\:\sqrt{\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}+\sqrt{{x}}}}\:+{C}= \\ $$$$=\left(\sqrt{{x}}−\mathrm{2}\right)\sqrt{\mathrm{1}−{x}}+\mathrm{arccos}\:\sqrt{{x}}\:+{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply