Question Number 122942 by CanovasCamiseros last updated on 21/Nov/20
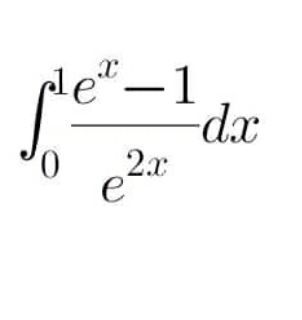
Commented by CanovasCamiseros last updated on 21/Nov/20
$$\boldsymbol{{help}}\:\boldsymbol{{please}} \\ $$
Answered by liberty last updated on 21/Nov/20
![∫_0 ^1 (e^(−x) −e^(−2x) ) dx = [−e^(−x) +(1/2)e^(−2x) ]_0 ^1 = (−e^(−1) +(1/2)e^(−2) )−(−1+(1/2)) = (1/2)−(1/e)+(1/(2e^2 )) = ((e^2 −2e+1)/(2e^2 ))=(1/2)(((e−1)/e))^2 .](https://www.tinkutara.com/question/Q122947.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left({e}^{−{x}} −{e}^{−\mathrm{2}{x}} \right)\:{dx}\:=\:\left[−{e}^{−{x}} +\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\mathrm{2}{x}} \:\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:=\:\left(−{e}^{−\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\mathrm{2}} \right)−\left(−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{e}}+\frac{\mathrm{1}}{\mathrm{2}{e}^{\mathrm{2}} }\:=\:\frac{{e}^{\mathrm{2}} −\mathrm{2}{e}+\mathrm{1}}{\mathrm{2}{e}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{e}−\mathrm{1}}{{e}}\right)^{\mathrm{2}} . \\ $$
Commented by CanovasCamiseros last updated on 21/Nov/20

$$\boldsymbol{{Thanks}}\:\boldsymbol{{sir}}! \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 21/Nov/20
![A =∫_0 ^1 ((e^x −1)/e^(2x) )dx changement e^x =t give A =∫_1 ^e ((t−1)/t^2 )(dt/t) =∫_1 ^e ((t−1)/t^3 )dt =∫_1 ^e (dt/t^2 )−∫_1 ^e t^(−3) dt =[−(1/t)]_1 ^e −[(1/(−3+1))t^(−3+1) ]_1 ^e =1−(1/e)+(1/2)[(1/t^2 )]_1 ^e =1−(1/e) +(1/2)(1−(1/e^2 ))](https://www.tinkutara.com/question/Q122993.png)
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}{\mathrm{e}^{\mathrm{2x}} }\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}\:=\int_{\mathrm{1}} ^{\mathrm{e}} \:\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\frac{\mathrm{dt}}{\mathrm{t}}\:=\int_{\mathrm{1}} ^{\mathrm{e}} \:\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }\mathrm{dt}\:=\int_{\mathrm{1}} ^{\mathrm{e}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }−\int_{\mathrm{1}} ^{\mathrm{e}} \:\mathrm{t}^{−\mathrm{3}} \:\mathrm{dt} \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{t}}\right]_{\mathrm{1}} ^{\mathrm{e}} \:−\left[\frac{\mathrm{1}}{−\mathrm{3}+\mathrm{1}}\mathrm{t}^{−\mathrm{3}+\mathrm{1}} \right]_{\mathrm{1}} ^{\mathrm{e}} \:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{e}}+\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\mathrm{e}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{e}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2}} }\right) \\ $$
