Question Number 122957 by I want to learn more last updated on 21/Nov/20
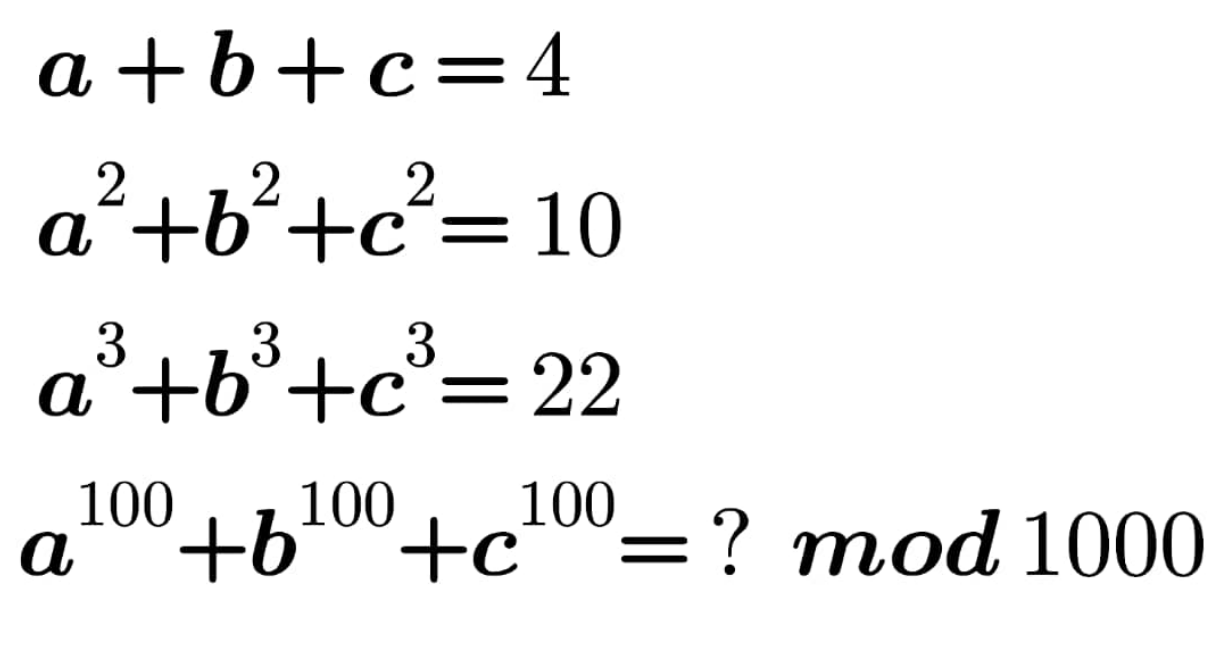
Commented by mr W last updated on 21/Nov/20

$${see}\:{Q}\mathrm{74970} \\ $$
Answered by mr W last updated on 21/Nov/20
![p_k =a^k +b^k +c^k e_1 =a+b+c e_2 =ab+bc+ca e_3 =abc e_(i≥4) =0 e_1 =p_1 =4 2e_2 =e_1 p_1 −p_2 =16−10=6 ⇒e_2 =3 3e_3 =e_2 p_1 −e_1 p_2 +p_3 =12−40+22=−6 ⇒e_3 =−2 0=e_3 p_1 −e_2 p_2 +e_1 p_3 −p_4 ⇒p_4 =−2×4−3×10+4×22=50 0=−e_3 p_2 +e_2 p_3 −e_1 p_4 +p_5 ⇒p_5 =−2×10−3×22+4×50=114 ...... p_n =4p_(n−1) −3p_(n−2) −2p_(n−3) z^3 −4z^2 +3z+2=0 (z−2)(z^2 −2z−1)=0 z=2, 1±(√2) ⇒p_n =a^n +b^n +c^n =2^n +(1+(√2))^n +(1−(√2))^n p_(100) =2^(100) +(1+(√2))^(100) +(1−(√2))^(100) =2^(100) +Σ_(k=0) ^(100) C_k ^(100) [((√2))^k +(−(√2))^k ] =(2^(10) )^(10) +Σ_(k=0) ^(50) C_(2k) ^(100) 2^(k+1) ......](https://www.tinkutara.com/question/Q122964.png)
$${p}_{{k}} ={a}^{{k}} +{b}^{{k}} +{c}^{{k}} \\ $$$${e}_{\mathrm{1}} ={a}+{b}+{c} \\ $$$${e}_{\mathrm{2}} ={ab}+{bc}+{ca} \\ $$$${e}_{\mathrm{3}} ={abc} \\ $$$${e}_{{i}\geqslant\mathrm{4}} =\mathrm{0} \\ $$$${e}_{\mathrm{1}} ={p}_{\mathrm{1}} =\mathrm{4} \\ $$$$\mathrm{2}{e}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −{p}_{\mathrm{2}} =\mathrm{16}−\mathrm{10}=\mathrm{6}\:\Rightarrow{e}_{\mathrm{2}} =\mathrm{3} \\ $$$$\mathrm{3}{e}_{\mathrm{3}} ={e}_{\mathrm{2}} {p}_{\mathrm{1}} −{e}_{\mathrm{1}} {p}_{\mathrm{2}} +{p}_{\mathrm{3}} =\mathrm{12}−\mathrm{40}+\mathrm{22}=−\mathrm{6}\:\Rightarrow{e}_{\mathrm{3}} =−\mathrm{2} \\ $$$$\mathrm{0}={e}_{\mathrm{3}} {p}_{\mathrm{1}} −{e}_{\mathrm{2}} {p}_{\mathrm{2}} +{e}_{\mathrm{1}} {p}_{\mathrm{3}} −{p}_{\mathrm{4}} \:\Rightarrow{p}_{\mathrm{4}} =−\mathrm{2}×\mathrm{4}−\mathrm{3}×\mathrm{10}+\mathrm{4}×\mathrm{22}=\mathrm{50} \\ $$$$\mathrm{0}=−{e}_{\mathrm{3}} {p}_{\mathrm{2}} +{e}_{\mathrm{2}} {p}_{\mathrm{3}} −{e}_{\mathrm{1}} {p}_{\mathrm{4}} +{p}_{\mathrm{5}} \:\Rightarrow{p}_{\mathrm{5}} =−\mathrm{2}×\mathrm{10}−\mathrm{3}×\mathrm{22}+\mathrm{4}×\mathrm{50}=\mathrm{114} \\ $$$$…… \\ $$$${p}_{{n}} =\mathrm{4}{p}_{{n}−\mathrm{1}} −\mathrm{3}{p}_{{n}−\mathrm{2}} −\mathrm{2}{p}_{{n}−\mathrm{3}} \\ $$$${z}^{\mathrm{3}} −\mathrm{4}{z}^{\mathrm{2}} +\mathrm{3}{z}+\mathrm{2}=\mathrm{0} \\ $$$$\left({z}−\mathrm{2}\right)\left({z}^{\mathrm{2}} −\mathrm{2}{z}−\mathrm{1}\right)=\mathrm{0} \\ $$$${z}=\mathrm{2},\:\mathrm{1}\pm\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{p}_{{n}} ={a}^{{n}} +{b}^{{n}} +{c}^{{n}} =\mathrm{2}^{{n}} +\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{n}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{{n}} \\ $$$${p}_{\mathrm{100}} =\mathrm{2}^{\mathrm{100}} +\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{100}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{\mathrm{100}} \\ $$$$=\mathrm{2}^{\mathrm{100}} +\underset{{k}=\mathrm{0}} {\overset{\mathrm{100}} {\sum}}{C}_{{k}} ^{\mathrm{100}} \left[\left(\sqrt{\mathrm{2}}\right)^{{k}} +\left(−\sqrt{\mathrm{2}}\right)^{{k}} \right] \\ $$$$=\left(\mathrm{2}^{\mathrm{10}} \right)^{\mathrm{10}} +\underset{{k}=\mathrm{0}} {\overset{\mathrm{50}} {\sum}}{C}_{\mathrm{2}{k}} ^{\mathrm{100}} \mathrm{2}^{{k}+\mathrm{1}} \\ $$$$…… \\ $$
Commented by I want to learn more last updated on 21/Nov/20
$$\mathrm{Wow},\:\mathrm{thanks}\:\mathrm{sir}.\:\mathrm{Hope}\:\mathrm{for}\:\mathrm{the}\:\mathrm{final}\:\mathrm{answer}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 23/Jul/21

$$\mathrm{Great} \\ $$
