Question Number 123009 by aurpeyz last updated on 21/Nov/20
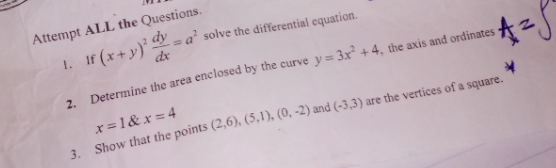
Commented by aurpeyz last updated on 21/Nov/20

$${pls}\:{help}\:{with}\:{question}\:\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 21/Nov/20
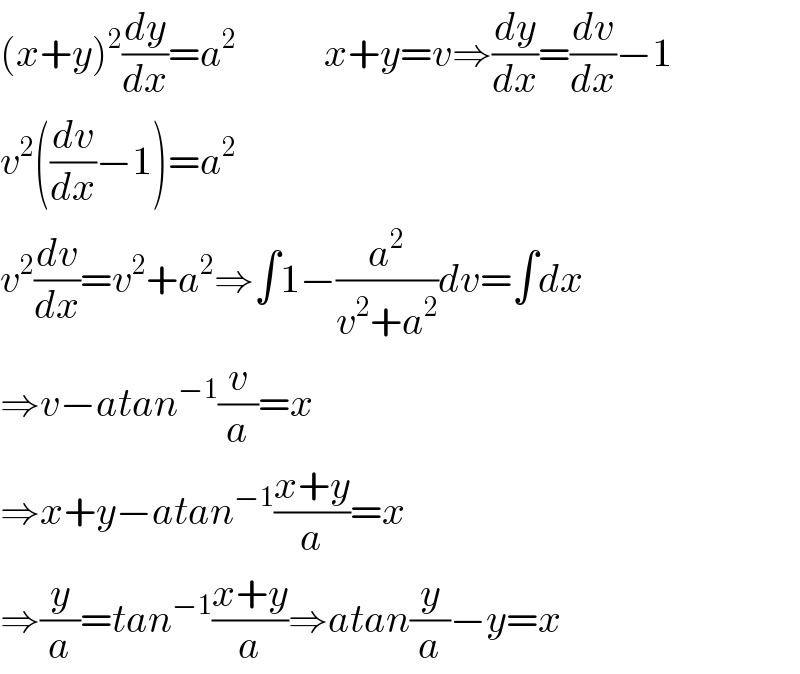
$$\left({x}+{y}\right)^{\mathrm{2}} \frac{{dy}}{{dx}}={a}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:{x}+{y}={v}\Rightarrow\frac{{dy}}{{dx}}=\frac{{dv}}{{dx}}−\mathrm{1} \\ $$$${v}^{\mathrm{2}} \left(\frac{{dv}}{{dx}}−\mathrm{1}\right)={a}^{\mathrm{2}} \\ $$$${v}^{\mathrm{2}} \frac{{dv}}{{dx}}={v}^{\mathrm{2}} +{a}^{\mathrm{2}} \Rightarrow\int\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{v}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dv}=\int{dx} \\ $$$$\Rightarrow{v}−{atan}^{−\mathrm{1}} \frac{{v}}{{a}}={x} \\ $$$$\Rightarrow{x}+{y}−{atan}^{−\mathrm{1}} \frac{{x}+{y}}{{a}}={x} \\ $$$$\Rightarrow\frac{{y}}{{a}}={tan}^{−\mathrm{1}} \frac{{x}+{y}}{{a}}\Rightarrow{atan}\frac{{y}}{{a}}−{y}={x} \\ $$
Commented by aurpeyz last updated on 22/Nov/20
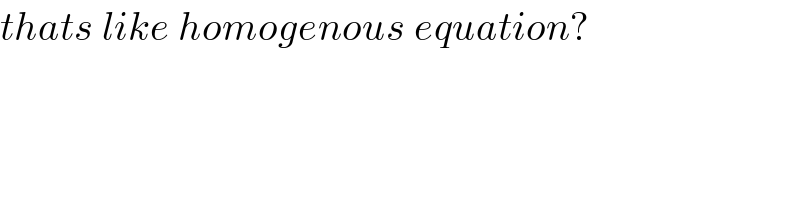
$${thats}\:{like}\:{homogenous}\:{equation}? \\ $$
