Question Number 123025 by ajfour last updated on 21/Nov/20
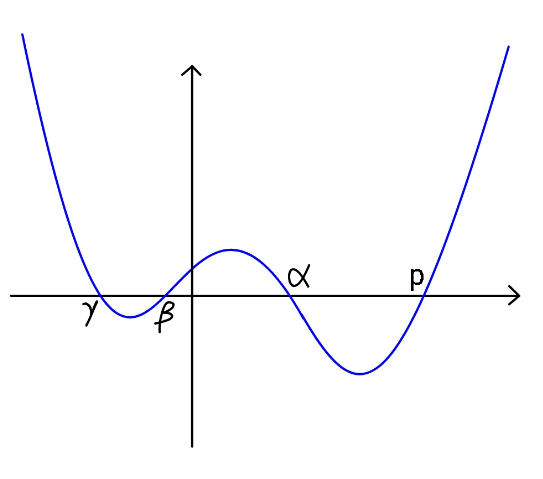
Commented by ajfour last updated on 22/Nov/20
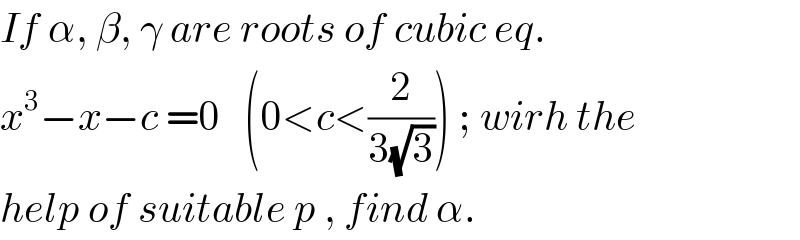
$${If}\:\alpha,\:\beta,\:\gamma\:{are}\:{roots}\:{of}\:{cubic}\:{eq}. \\ $$$${x}^{\mathrm{3}} −{x}−{c}\:=\mathrm{0}\:\:\:\left(\mathrm{0}<{c}<\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\right)\:;\:{wirh}\:{the} \\ $$$${help}\:{of}\:{suitable}\:{p}\:,\:{find}\:\alpha. \\ $$
Commented by ajfour last updated on 22/Nov/20

$${value}\:{of}\:{p}\:{is}\:{to}\:{be}\:{chosen},\:{so} \\ $$$${that}\:{the}\:{degree}\:{four}\:{can}\:{be}\:{solved} \\ $$$${if}\:{not}\:{the}\:{degree}\:{three}. \\ $$
Commented by mr W last updated on 22/Nov/20
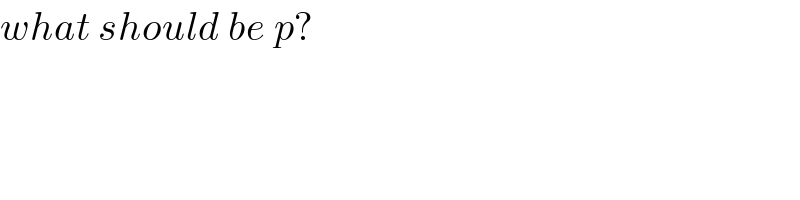
$${what}\:{should}\:{be}\:{p}? \\ $$
Commented by MJS_new last updated on 22/Nov/20

$$\mathrm{just}\:\mathrm{a}\:\mathrm{few}\:\mathrm{thoughts}… \\ $$$$\mathrm{if}\:\alpha>\mathrm{0}\wedge\beta<\mathrm{0}\wedge\gamma<\mathrm{0}\wedge\beta\neq\gamma\:\Rightarrow\:\alpha=−\left(\beta+\gamma\right) \\ $$$${x}^{\mathrm{3}} +{px}+{q}=\mathrm{0}\:\mathrm{with}\:{p}=−\mathrm{1}\:\Rightarrow\:\beta=−\frac{\gamma}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{4}−\mathrm{3}\gamma^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow\:{c}=\gamma\left(\gamma^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\mathrm{introducing}\:{p}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left({x}−{p}\right)\left({x}−\gamma\right)\left({x}−\frac{\gamma}{\mathrm{2}}−\frac{\sqrt{\mathrm{4}−\mathrm{3}\gamma^{\mathrm{2}} }}{\mathrm{2}}\right)\left(−\frac{\gamma}{\mathrm{2}}+\frac{\sqrt{\mathrm{4}−\mathrm{3}\gamma^{\mathrm{2}} }}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{it}\:\mathrm{would}\:\mathrm{be}\:\mathrm{nice}\:\mathrm{if}\:{p}=−\gamma \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:{c}=\gamma\left(\gamma^{\mathrm{2}} −\mathrm{1}\right)\:\mathrm{for}\:\gamma\:\mathrm{but}\:\mathrm{this} \\ $$$$\mathrm{is}\:\mathrm{exactly}\:\mathrm{the}\:\mathrm{same}\:\mathrm{problem}\:\mathrm{as}\:\mathrm{before}: \\ $$$$\gamma^{\mathrm{3}} −\gamma−{c}=\mathrm{0} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{any}\:\mathrm{fitting}\:{p}\:\mathrm{without} \\ $$$$\mathrm{solving}\:\mathrm{this}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{polynome}… \\ $$
Answered by ajfour last updated on 26/Nov/20

