Question-123034

Question Number 123034 by benjo_mathlover last updated on 21/Nov/20

Answered by mathmax by abdo last updated on 21/Nov/20

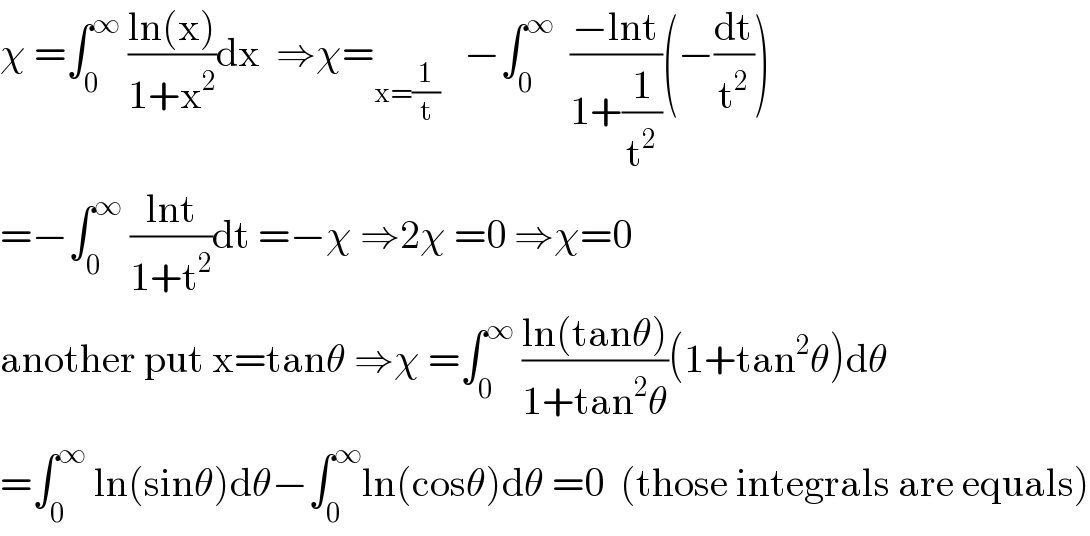
χ =∫_0 ^∞ ((ln(x))/(1+x^2 ))dx ⇒χ=_(x=(1/t)) −∫_0 ^∞ ((−lnt)/(1+(1/t^2 )))(−(dt/t^2 )) =−∫_0 ^∞ ((lnt)/(1+t^2 ))dt =−χ ⇒2χ =0 ⇒χ=0 another put x=tanθ ⇒χ =∫_0 ^∞ ((ln(tanθ))/(1+tan^2 θ))(1+tan^2 θ)dθ =∫_0 ^∞ ln(sinθ)dθ−∫_0 ^∞ ln(cosθ)dθ =0 (those integrals are equals)

$$\chi\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:\Rightarrow\chi=_{\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}} \:\:\:−\int_{\mathrm{0}} ^{\infty} \:\:\frac{−\mathrm{lnt}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\left(−\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right) \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=−\chi\:\Rightarrow\mathrm{2}\chi\:=\mathrm{0}\:\Rightarrow\chi=\mathrm{0} \\ $$$$\mathrm{another}\:\mathrm{put}\:\mathrm{x}=\mathrm{tan}\theta\:\Rightarrow\chi\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{tan}\theta\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)\mathrm{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{ln}\left(\mathrm{sin}\theta\right)\mathrm{d}\theta−\int_{\mathrm{0}} ^{\infty} \mathrm{ln}\left(\mathrm{cos}\theta\right)\mathrm{d}\theta\:=\mathrm{0}\:\:\left(\mathrm{those}\:\mathrm{integrals}\:\mathrm{are}\:\mathrm{equals}\right) \\ $$

Facebook Tweet Pin

Question-123034

Leave a Reply Cancel reply