Question Number 123141 by ajfour last updated on 23/Nov/20

Commented by ajfour last updated on 23/Nov/20
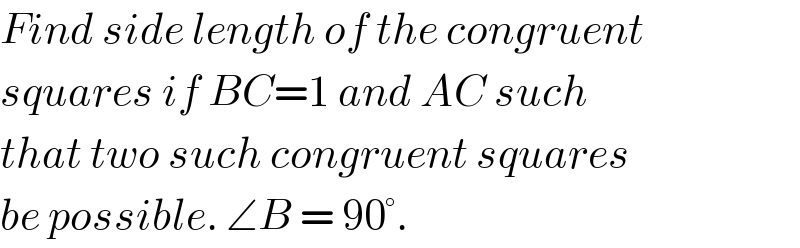
$${Find}\:{side}\:{length}\:{of}\:{the}\:{congruent} \\ $$$${squares}\:{if}\:{BC}=\mathrm{1}\:{and}\:{AC}\:{such} \\ $$$${that}\:{two}\:{such}\:{congruent}\:{squares} \\ $$$${be}\:{possible}.\:\angle{B}\:=\:\mathrm{90}°. \\ $$
Answered by mr W last updated on 23/Nov/20
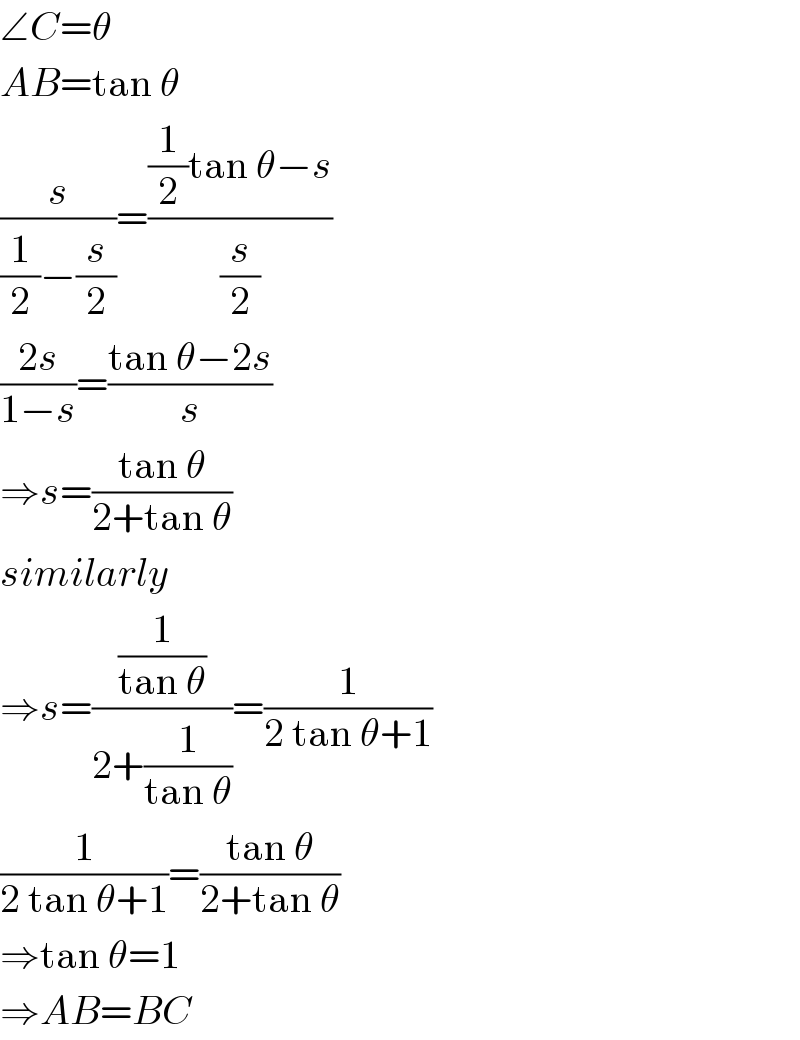
$$\angle{C}=\theta \\ $$$${AB}=\mathrm{tan}\:\theta \\ $$$$\frac{{s}}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{{s}}{\mathrm{2}}}=\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:\theta−{s}}{\frac{{s}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{2}{s}}{\mathrm{1}−{s}}=\frac{\mathrm{tan}\:\theta−\mathrm{2}{s}}{{s}} \\ $$$$\Rightarrow{s}=\frac{\mathrm{tan}\:\theta}{\mathrm{2}+\mathrm{tan}\:\theta} \\ $$$${similarly} \\ $$$$\Rightarrow{s}=\frac{\frac{\mathrm{1}}{\mathrm{tan}\:\theta}}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{tan}\:\theta}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{tan}\:\theta+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{tan}\:\theta+\mathrm{1}}=\frac{\mathrm{tan}\:\theta}{\mathrm{2}+\mathrm{tan}\:\theta} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\mathrm{1} \\ $$$$\Rightarrow{AB}={BC} \\ $$
Commented by ajfour last updated on 23/Nov/20
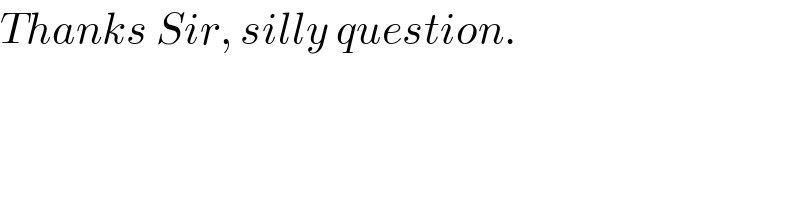
$${Thanks}\:{Sir},\:{silly}\:{question}. \\ $$
