Question Number 123154 by liberty last updated on 23/Nov/20

Answered by benjo_mathlover last updated on 23/Nov/20
![let t=sin q ⇒dt = cos q dq η (x)= ∫ (√(1−sin^2 q)) (cos q dq) η (x)= ∫(((1+cos 2q)/2)) dq η (x)= ((q+(1/2)sin 2q)/2) + c = ((sin^(−1) (t)+t(√(1−t^2 )))/2) + c thus η = ∫_1 ^(cosh (x)) (√(1−t^2 )) dt =[ ((sin^(−1) (t)+t(√(1−t^2 )) )/2)]_1 ^(cosh (x)) = [((sin^(−1) (cosh (x))+cosh (x)sinh (x))/2)] − (π/4)](https://www.tinkutara.com/question/Q123164.png)
$$\:{let}\:{t}=\mathrm{sin}\:\:{q}\:\Rightarrow{dt}\:=\:\mathrm{cos}\:{q}\:{dq} \\ $$$$\eta\:\left({x}\right)=\:\int\:\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {q}}\:\left(\mathrm{cos}\:{q}\:{dq}\right) \\ $$$$\eta\:\left({x}\right)=\:\int\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{q}}{\mathrm{2}}\right)\:{dq}\: \\ $$$$\eta\:\left({x}\right)=\:\frac{{q}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{q}}{\mathrm{2}}\:+\:{c}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{sin}^{−\mathrm{1}} \left({t}\right)+{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{2}}\:+\:{c} \\ $$$${thus}\:\eta\:=\:\underset{\mathrm{1}} {\overset{\mathrm{cosh}\:\left({x}\right)} {\int}}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt}\: \\ $$$$\:=\left[\:\frac{\mathrm{sin}^{−\mathrm{1}} \left({t}\right)+{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:}{\mathrm{2}}\right]_{\mathrm{1}} ^{\mathrm{cosh}\:\left({x}\right)} \\ $$$$\:=\:\left[\frac{\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{cosh}\:\left({x}\right)\right)+\mathrm{cosh}\:\left({x}\right)\mathrm{sinh}\:\left({x}\right)}{\mathrm{2}}\right]\:−\:\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 23/Nov/20
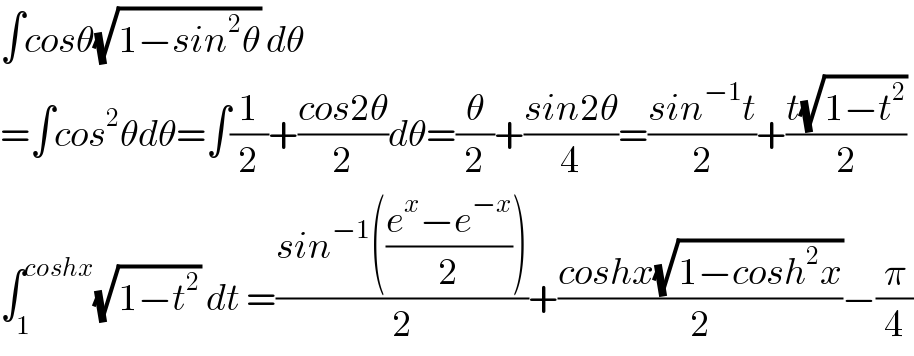
$$\int{cos}\theta\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$=\int{cos}^{\mathrm{2}} \theta{d}\theta=\int\frac{\mathrm{1}}{\mathrm{2}}+\frac{{cos}\mathrm{2}\theta}{\mathrm{2}}{d}\theta=\frac{\theta}{\mathrm{2}}+\frac{{sin}\mathrm{2}\theta}{\mathrm{4}}=\frac{{sin}^{−\mathrm{1}} {t}}{\mathrm{2}}+\frac{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\int_{\mathrm{1}} ^{{coshx}} \sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt}\:=\frac{{sin}^{−\mathrm{1}} \left(\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}}\right)}{\mathrm{2}}+\frac{{coshx}\sqrt{\mathrm{1}−{cosh}^{\mathrm{2}} {x}}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 23/Nov/20
![f(x)=∫_1 ^((e^x +e^(−x) )/2) (√(1−t^2 ))dt ⇒f(x)=_(t=sinθ) ∫_(π/2) ^(arcsin(((e^x +e^(−x) )/2))) cosθ cosθ dθ =(1/2)∫_(π/2) ^(arcsin(((e^x +e^(−x) )/2))) (1+cos(2θ))dθ =(1/2)[θ]_(π/2) ^(arcsin(((e^x +e^(−x) )/2))) +(1/4)[sin(2θ)]_(π/2) ^(arcsin(((e^x +e^(−x) )/2))) =(1/2){arcsin(((e^x +e^(−x) )/2))−(π/2)) +(1/2)[sinθ(√(1−sin^2 θ))]_(π/2) ^(arcsin(((e^x +e^(−x) )/2))) f(x)=(1/2)( arcsin(((e^x +e^(−x) )/2)))−(π/4) +(1/2)(((e^x +e^(−x) )/2)(√(1−(((e^x +e^(−x) )/2))^2 )))](https://www.tinkutara.com/question/Q123197.png)
$$\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{1}} ^{\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}} \sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=_{\mathrm{t}=\mathrm{sin}\theta} \:\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{arcsin}\left(\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\right)} \mathrm{cos}\theta\:\mathrm{cos}\theta\:\mathrm{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{arcsin}\left(\frac{\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\right)} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)\right)\mathrm{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\theta\right]_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{arcsin}\left(\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\right)} +\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{sin}\left(\mathrm{2}\theta\right)\right]_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{arcsin}\left(\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{arcsin}\left(\frac{\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\right)−\frac{\pi}{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{sin}\theta\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta}\right]_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{arcsin}\left(\frac{\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\right)} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\:\mathrm{arcsin}\left(\frac{\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\right)\right)−\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\sqrt{\mathrm{1}−\left(\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\right)^{\mathrm{2}} }\right) \\ $$$$ \\ $$
