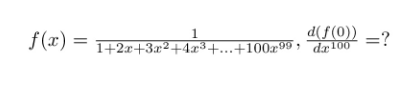
Question Number 123155 by Algoritm last updated on 23/Nov/20
Answered by Dwaipayan Shikari last updated on 23/Nov/20
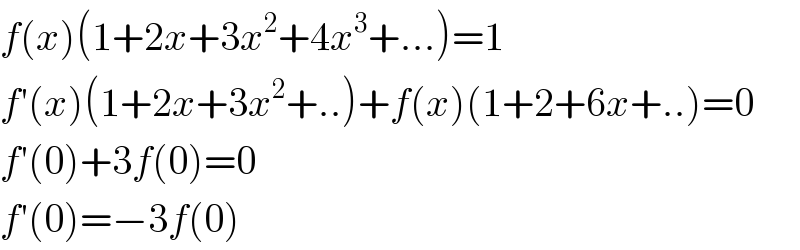
$${f}\left({x}\right)\left(\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +…\right)=\mathrm{1} \\ $$$${f}'\left({x}\right)\left(\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +..\right)+{f}\left({x}\right)\left(\mathrm{1}+\mathrm{2}+\mathrm{6}{x}+..\right)=\mathrm{0} \\ $$$${f}'\left(\mathrm{0}\right)+\mathrm{3}{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}'\left(\mathrm{0}\right)=−\mathrm{3}{f}\left(\mathrm{0}\right) \\ $$
