Menu Close

Question-123210

Tinku Tara 0 Comments
Pin




Question Number 123210 by Khalmohmmad last updated on 24/Nov/20
Answered by Lordose last updated on 24/Nov/20
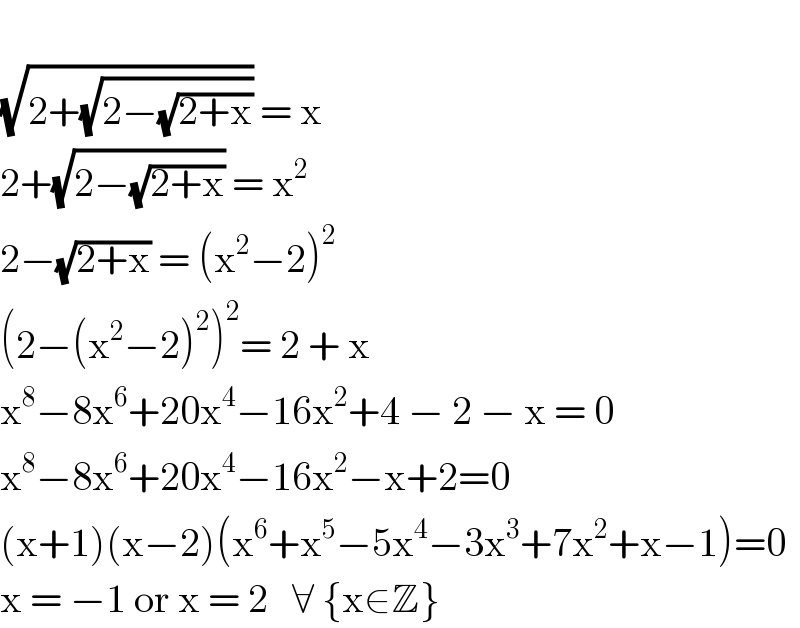
(√(2+(√(2−(√(2+x)))))) = x 2+(√(2−(√(2+x)))) = x^2 2−(√(2+x)) = (x^2 −2)^2 (2−(x^2 −2)^2 )^2 = 2 + x x^8 −8x^6 +20x^4 −16x^2 +4 − 2 − x = 0 x^8 −8x^6 +20x^4 −16x^2 −x+2=0 (x+1)(x−2)(x^6 +x^5 −5x^4 −3x^3 +7x^2 +x−1)=0 x = −1 or x = 2 ∀ {x∈Z}
$$ \\ $$$$\sqrt{\mathrm{2}+\sqrt{\mathrm{2}−\sqrt{\mathrm{2}+\mathrm{x}}}}\:=\:\mathrm{x} \\ $$$$\mathrm{2}+\sqrt{\mathrm{2}−\sqrt{\mathrm{2}+\mathrm{x}}}\:=\:\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{2}−\sqrt{\mathrm{2}+\mathrm{x}}\:=\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{2}−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} \right)^{\mathrm{2}} =\:\mathrm{2}\:+\:\mathrm{x} \\ $$$$\mathrm{x}^{\mathrm{8}} −\mathrm{8x}^{\mathrm{6}} +\mathrm{20x}^{\mathrm{4}} −\mathrm{16x}^{\mathrm{2}} +\mathrm{4}\:−\:\mathrm{2}\:−\:\mathrm{x}\:=\:\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{8}} −\mathrm{8x}^{\mathrm{6}} +\mathrm{20x}^{\mathrm{4}} −\mathrm{16x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{6}} +\mathrm{x}^{\mathrm{5}} −\mathrm{5x}^{\mathrm{4}} −\mathrm{3x}^{\mathrm{3}} +\mathrm{7x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{x}\:=\:−\mathrm{1}\:\mathrm{or}\:\mathrm{x}\:=\:\mathrm{2}\:\:\:\forall\:\left\{\mathrm{x}\in\mathbb{Z}\right\} \\ $$
Commented by MJS_new last updated on 24/Nov/20
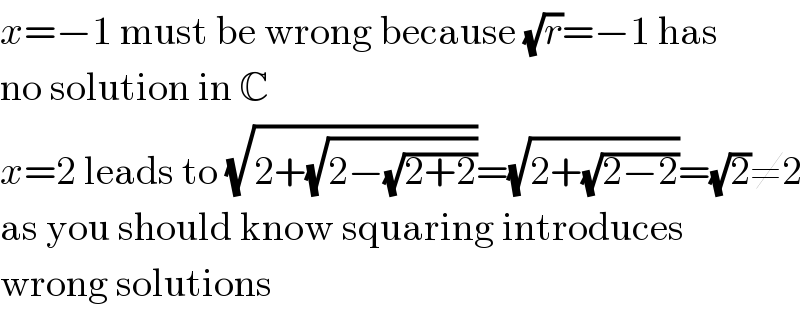
x=−1 must be wrong because (√r)=−1 has no solution in C x=2 leads to (√(2+(√(2−(√(2+2))))))=(√(2+(√(2−2))))=(√2)≠2 as you should know squaring introduces wrong solutions
$${x}=−\mathrm{1}\:\mathrm{must}\:\mathrm{be}\:\mathrm{wrong}\:\mathrm{because}\:\sqrt{{r}}=−\mathrm{1}\:\mathrm{has} \\ $$$$\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathbb{C} \\ $$$${x}=\mathrm{2}\:\mathrm{leads}\:\mathrm{to}\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}−\sqrt{\mathrm{2}+\mathrm{2}}}}=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}−\mathrm{2}}}=\sqrt{\mathrm{2}}\neq\mathrm{2} \\ $$$$\mathrm{as}\:\mathrm{you}\:\mathrm{should}\:\mathrm{know}\:\mathrm{squaring}\:\mathrm{introduces} \\ $$$$\mathrm{wrong}\:\mathrm{solutions} \\ $$
Commented by 676597498 last updated on 24/Nov/20
true
$${true} \\ $$
Commented by MJS_new last updated on 24/Nov/20
x^6 +x^5 −5x^4 −3x^3 +7x^2 +x−1=0 (x^3 −3x+1)(x^3 +x^2 −2x−1)=0 solving both using the trigonometric method and testing the solutions we get x_1 =−2cos (π/9) false x_2 =2sin (π/(18)) false x_3 =2cos ((2π)/9) true x_4 =−(1/3)−((2(√7))/3)cos ((π/6)+(1/3)arcsin ((√7)/(14))) false x_5 =−(1/3)−((2(√7))/3)sin ((1/3)arcsin ((√7)/(14))) false x_6 =−(1/3)+((2(√7))/3)sin ((π/3)+(1/3)arcsin ((√7)/(14))) false ⇒ x=2cos ((2π)/9)
$${x}^{\mathrm{6}} +{x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{7}{x}^{\mathrm{2}} +{x}−\mathrm{1}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{3}} −\mathrm{3}{x}+\mathrm{1}\right)\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{solving}\:\mathrm{both}\:\mathrm{using}\:\mathrm{the}\:\mathrm{trigonometric}\:\mathrm{method} \\ $$$$\mathrm{and}\:\mathrm{testing}\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{we}\:\mathrm{get} \\ $$$${x}_{\mathrm{1}} =−\mathrm{2cos}\:\frac{\pi}{\mathrm{9}}\:\mathrm{false} \\ $$$${x}_{\mathrm{2}} =\mathrm{2sin}\:\frac{\pi}{\mathrm{18}}\:\mathrm{false} \\ $$$${x}_{\mathrm{3}} =\mathrm{2cos}\:\frac{\mathrm{2}\pi}{\mathrm{9}}\:\mathrm{true} \\ $$$${x}_{\mathrm{4}} =−\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right)\:\mathrm{false} \\ $$$${x}_{\mathrm{5}} =−\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right)\:\mathrm{false} \\ $$$${x}_{\mathrm{6}} =−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right)\:\mathrm{false} \\ $$$$\Rightarrow\:{x}=\mathrm{2cos}\:\frac{\mathrm{2}\pi}{\mathrm{9}} \\ $$
Commented by Lordose last updated on 24/Nov/20
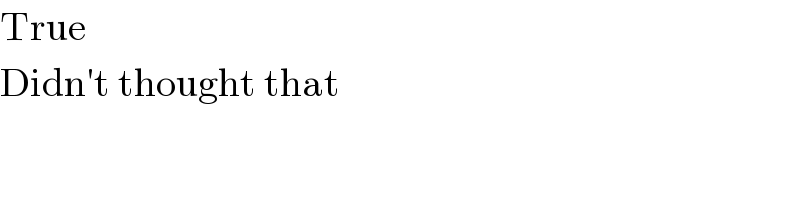
True Didn′t thought that
$$\mathrm{True} \\ $$$$\mathrm{Didn}'\mathrm{t}\:\mathrm{thought}\:\mathrm{that} \\ $$
Commented by Lordose last updated on 24/Nov/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by Khalmohmmad last updated on 24/Nov/20
Thanks sir
$${Thanks}\:\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 24/Nov/20
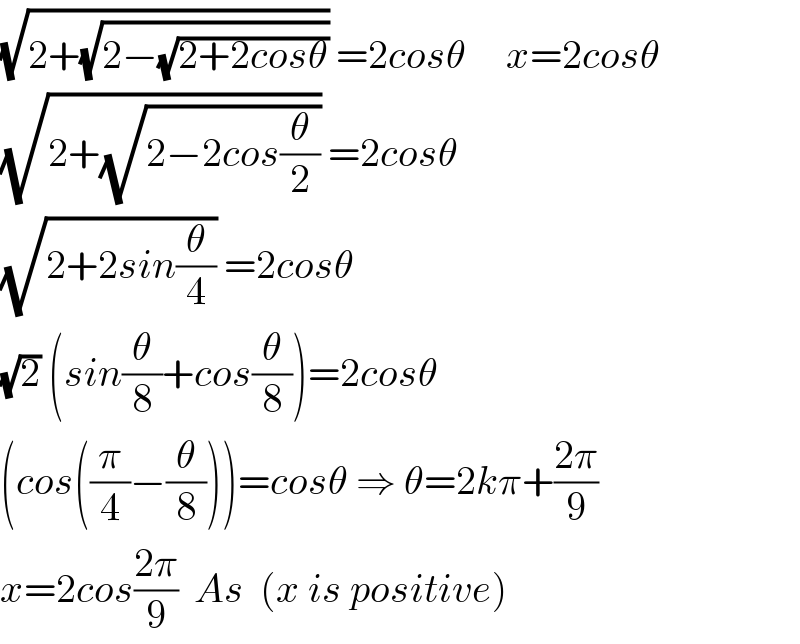
(√(2+(√(2−(√(2+2cosθ)))))) =2cosθ x=2cosθ (√(2+(√(2−2cos(θ/2))))) =2cosθ (√(2+2sin(θ/4))) =2cosθ (√2) (sin(θ/8)+cos(θ/8))=2cosθ (cos((π/4)−(θ/8)))=cosθ ⇒ θ=2kπ+((2π)/9) x=2cos((2π)/9) As (x is positive)
$$\sqrt{\mathrm{2}+\sqrt{\mathrm{2}−\sqrt{\mathrm{2}+\mathrm{2}{cos}\theta}}}\:=\mathrm{2}{cos}\theta\:\:\:\:\:{x}=\mathrm{2}{cos}\theta \\ $$$$\sqrt{\mathrm{2}+\sqrt{\mathrm{2}−\mathrm{2}{cos}\frac{\theta}{\mathrm{2}}}}\:=\mathrm{2}{cos}\theta \\ $$$$\sqrt{\mathrm{2}+\mathrm{2}{sin}\frac{\theta}{\mathrm{4}}}\:=\mathrm{2}{cos}\theta \\ $$$$\sqrt{\mathrm{2}}\:\left({sin}\frac{\theta}{\mathrm{8}}+{cos}\frac{\theta}{\mathrm{8}}\right)=\mathrm{2}{cos}\theta \\ $$$$\left({cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{8}}\right)\right)={cos}\theta\:\Rightarrow\:\theta=\mathrm{2}{k}\pi+\frac{\mathrm{2}\pi}{\mathrm{9}} \\ $$$${x}=\mathrm{2}{cos}\frac{\mathrm{2}\pi}{\mathrm{9}}\:\:{As}\:\:\left({x}\:{is}\:{positive}\right) \\ $$
Commented by Khalmohmmad last updated on 24/Nov/20
Thanks sir
$${Thanks}\:\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *