Question Number 123385 by help last updated on 25/Nov/20
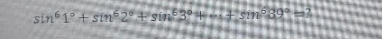
Answered by Dwaipayan Shikari last updated on 25/Nov/20
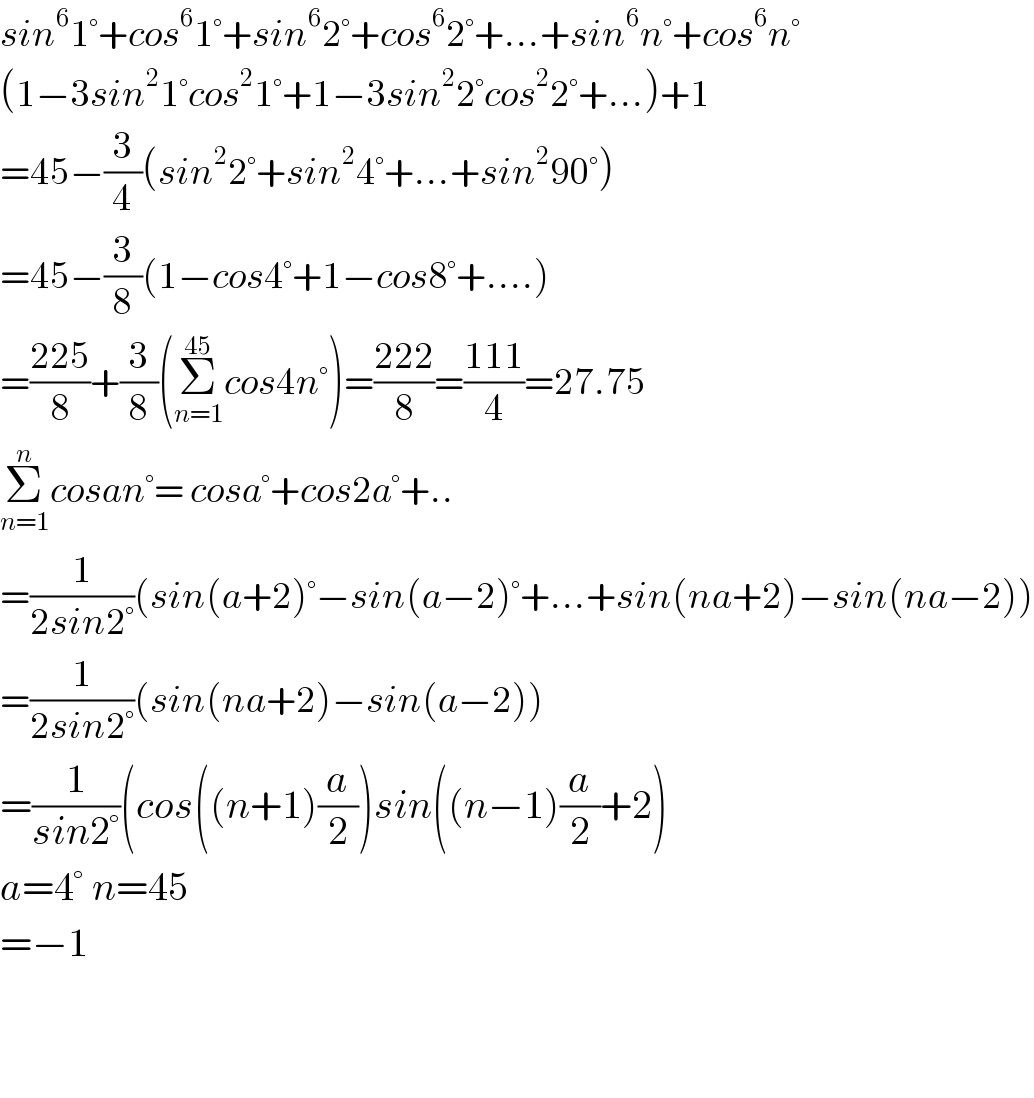
$${sin}^{\mathrm{6}} \mathrm{1}°+{cos}^{\mathrm{6}} \mathrm{1}°+{sin}^{\mathrm{6}} \mathrm{2}°+{cos}^{\mathrm{6}} \mathrm{2}°+…+{sin}^{\mathrm{6}} {n}°+{cos}^{\mathrm{6}} {n}° \\ $$$$\left(\mathrm{1}−\mathrm{3}{sin}^{\mathrm{2}} \mathrm{1}°{cos}^{\mathrm{2}} \mathrm{1}°+\mathrm{1}−\mathrm{3}{sin}^{\mathrm{2}} \mathrm{2}°{cos}^{\mathrm{2}} \mathrm{2}°+…\right)+\mathrm{1} \\ $$$$=\mathrm{45}−\frac{\mathrm{3}}{\mathrm{4}}\left({sin}^{\mathrm{2}} \mathrm{2}°+{sin}^{\mathrm{2}} \mathrm{4}°+…+{sin}^{\mathrm{2}} \mathrm{90}°\right) \\ $$$$=\mathrm{45}−\frac{\mathrm{3}}{\mathrm{8}}\left(\mathrm{1}−{cos}\mathrm{4}°+\mathrm{1}−{cos}\mathrm{8}°+….\right) \\ $$$$=\frac{\mathrm{225}}{\mathrm{8}}+\frac{\mathrm{3}}{\mathrm{8}}\left(\underset{{n}=\mathrm{1}} {\overset{\mathrm{45}} {\sum}}{cos}\mathrm{4}{n}°\right)=\frac{\mathrm{222}}{\mathrm{8}}=\frac{\mathrm{111}}{\mathrm{4}}=\mathrm{27}.\mathrm{75} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{cosan}°=\:{cosa}°+{cos}\mathrm{2}{a}°+.. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{sin}\mathrm{2}°}\left({sin}\left({a}+\mathrm{2}\right)°−{sin}\left({a}−\mathrm{2}\right)°+…+{sin}\left({na}+\mathrm{2}\right)−{sin}\left({na}−\mathrm{2}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{sin}\mathrm{2}°}\left({sin}\left({na}+\mathrm{2}\right)−{sin}\left({a}−\mathrm{2}\right)\right) \\ $$$$=\frac{\mathrm{1}}{{sin}\mathrm{2}°}\left({cos}\left(\left({n}+\mathrm{1}\right)\frac{{a}}{\mathrm{2}}\right){sin}\left(\left({n}−\mathrm{1}\right)\frac{{a}}{\mathrm{2}}+\mathrm{2}\right)\right. \\ $$$${a}=\mathrm{4}°\:{n}=\mathrm{45} \\ $$$$=−\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
