Question Number 123528 by ajfour last updated on 26/Nov/20
Commented by ajfour last updated on 26/Nov/20
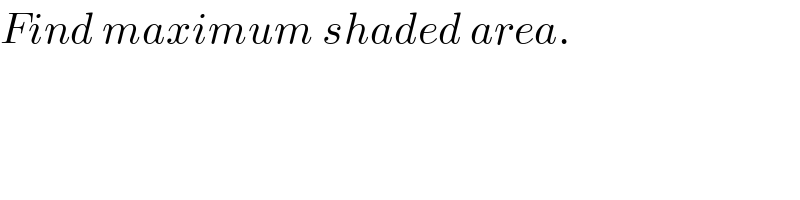
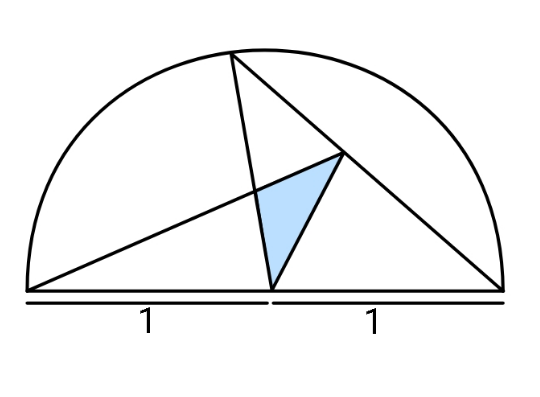
$${Find}\:{maximum}\:{shaded}\:{area}. \\ $$
Answered by mr W last updated on 26/Nov/20
Commented by ajfour last updated on 26/Nov/20
![eq. of BC y=m(1−x) let y_D =q , x_D =1−(q/m) eq. of AD y=((q(x+1))/((2−(q/m)))) eq. of OC y=((−2mx)/((1−m^2 ))) For E(p , y_E ) ((q(p+1))/((2−(q/m))))=((−2mp)/(1−m^2 )) p=((−((q/(2−(q/m)))))/((q/((2−(q/m))))+((2m)/(1−m^2 )))) y_E =(((((2m)/(1−m^2 )))((q/(2−(q/m)))))/((q/((2−(q/m))))+((2m)/(1−m^2 )))) y_E = ((2qm)/(q(1−m^2 )+4m−2q)) 2△=y_D −y_E = q−((2qm)/(q(1−m^2 )+4m−2q)) .................................................. 2△ = ((2mq−q^2 (1+m^2 ))/(4m−q(1+m^2 ))) .................................................. ((∂(2△))/∂q)=(([2m−2q(1+m^2 )][4m−q(1+m^2 )]+(1+m^2 )[2mq−q^2 (1+m^2 )])/({4m−q(1+m^2 )]^2 ))=0 ⇒ 8m^2 −8mq(1+m^2 )+q^2 (1+m^2 )^2 =0 ............(I) & ((∂(2△))/∂m)=0 ⇒ (2q−2mq^2 )[4m−q(1+m^2 )] = (4−2qm)[2mq−q^2 (1+m^2 )] ⇒ 8mq−2q^2 (1+m^2 )−8m^2 q^2 +2mq^3 (1+m^2 )=8mq−4q^2 (1+m^2 ) −4m^2 q^2 +2mq^3 (1+m^2 ) ⇒ 4m^2 q^2 −2q^2 (1+m^2 )=0 ⇒ 3m^2 =2 ⇒ m=(√(2/3)) And from (I) 8((2/3))−8q(1+(2/3))(√(2/3)) +q^2 (1+(2/3))^2 =0 ⇒ ((25q^2 )/9)−((40(√2)q)/(3(√3)))+((16)/3)=0 ⇒ 25q^2 −40(√6)q+48=0 q=((4(√6))/5)−((√(96−48))/5) = ((4((√6)−(√3)))/5) q ≈ 0.57395 2△=((2mq−q^2 (1+m^2 ))/(4m−q(1+m^2 ))) △= (4/2)((((√6)−(√3))/5)){((2(√(2/3))−((20)/3)((((√6)−(√3))/5)))/(4(√(2/3))−((20)/3)((((√6)−(√3))/5))))} = ((2((√6)−(√3)))/5)(((2(√6)−4(√6)+4(√3))/(4(√6)−4(√6)+4(√3)))) = ((2((√6)−(√3)))/5)(((4(√3)+2(√6))/(4(√3)))) =((((√2)−1)(2(√3)+(√6)))/5) △ = ((√6)/5) sq. units ★ △≈ 0.489897949 % shaded area = ((40(√6))/π) ≈ 31.187872](https://www.tinkutara.com/question/Q123546.png)
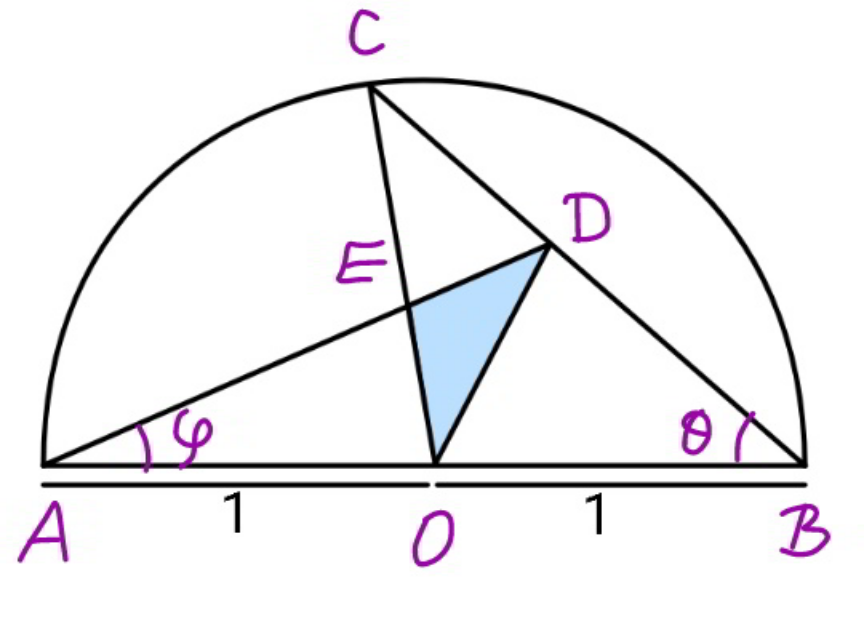
$${eq}.\:{of}\:{BC} \\ $$$${y}={m}\left(\mathrm{1}−{x}\right) \\ $$$${let}\:\:\:{y}_{{D}} ={q}\:,\:\:{x}_{{D}} =\mathrm{1}−\frac{{q}}{{m}} \\ $$$${eq}.\:{of}\:{AD} \\ $$$${y}=\frac{{q}\left({x}+\mathrm{1}\right)}{\left(\mathrm{2}−\frac{{q}}{{m}}\right)} \\ $$$${eq}.\:{of}\:{OC} \\ $$$${y}=\frac{−\mathrm{2}{mx}}{\left(\mathrm{1}−{m}^{\mathrm{2}} \right)} \\ $$$${For}\:{E}\left({p}\:,\:{y}_{{E}} \right) \\ $$$$\frac{{q}\left({p}+\mathrm{1}\right)}{\left(\mathrm{2}−\frac{{q}}{{m}}\right)}=\frac{−\mathrm{2}{mp}}{\mathrm{1}−{m}^{\mathrm{2}} } \\ $$$${p}=\frac{−\left(\frac{{q}}{\mathrm{2}−\frac{{q}}{{m}}}\right)}{\frac{{q}}{\left(\mathrm{2}−\frac{{q}}{{m}}\right)}+\frac{\mathrm{2}{m}}{\mathrm{1}−{m}^{\mathrm{2}} }} \\ $$$$ \\ $$$${y}_{{E}} =\frac{\left(\frac{\mathrm{2}{m}}{\mathrm{1}−{m}^{\mathrm{2}} }\right)\left(\frac{{q}}{\mathrm{2}−\frac{{q}}{{m}}}\right)}{\frac{{q}}{\left(\mathrm{2}−\frac{{q}}{{m}}\right)}+\frac{\mathrm{2}{m}}{\mathrm{1}−{m}^{\mathrm{2}} }} \\ $$$$\:{y}_{{E}} \:=\:\frac{\mathrm{2}{qm}}{{q}\left(\mathrm{1}−{m}^{\mathrm{2}} \right)+\mathrm{4}{m}−\mathrm{2}{q}} \\ $$$$\mathrm{2}\bigtriangleup={y}_{{D}} −{y}_{{E}} \\ $$$$\:\:\:=\:\:{q}−\frac{\mathrm{2}{qm}}{{q}\left(\mathrm{1}−{m}^{\mathrm{2}} \right)+\mathrm{4}{m}−\mathrm{2}{q}} \\ $$$$\:………………………………………….. \\ $$$$\:\mathrm{2}\bigtriangleup\:=\:\frac{\mathrm{2}{mq}−{q}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{\mathrm{4}{m}−{q}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)} \\ $$$$\:………………………………………….. \\ $$$$\frac{\partial\left(\mathrm{2}\bigtriangleup\right)}{\partial{q}}=\frac{\left[\mathrm{2}{m}−\mathrm{2}{q}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\right]\left[\mathrm{4}{m}−{q}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\right]+\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left[\mathrm{2}{mq}−{q}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)\right]}{\left\{\mathrm{4}{m}−{q}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\right]^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{8}{m}^{\mathrm{2}} −\mathrm{8}{mq}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)+{q}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:…………\left(\boldsymbol{{I}}\right)\:\:\:\:\:\:\:\& \\ $$$$\frac{\partial\left(\mathrm{2}\bigtriangleup\right)}{\partial{m}}=\mathrm{0} \\ $$$$\Rightarrow\:\:\left(\mathrm{2}{q}−\mathrm{2}{mq}^{\mathrm{2}} \right)\left[\mathrm{4}{m}−{q}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\right] \\ $$$$\:\:\:\:\:=\:\left(\mathrm{4}−\mathrm{2}{qm}\right)\left[\mathrm{2}{mq}−{q}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)\right] \\ $$$$\Rightarrow\: \\ $$$$\mathrm{8}{mq}−\mathrm{2}{q}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)−\mathrm{8}{m}^{\mathrm{2}} {q}^{\mathrm{2}} \\ $$$$+\mathrm{2}{mq}^{\mathrm{3}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)=\mathrm{8}{mq}−\mathrm{4}{q}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right) \\ $$$$−\mathrm{4}{m}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{2}{mq}^{\mathrm{3}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right) \\ $$$$\Rightarrow \\ $$$$\mathrm{4}{m}^{\mathrm{2}} {q}^{\mathrm{2}} −\mathrm{2}{q}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\mathrm{3}{m}^{\mathrm{2}} =\mathrm{2} \\ $$$$\Rightarrow\:\:\:\boldsymbol{{m}}=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\:\:\: \\ $$$${And}\:\:{from}\:\left(\boldsymbol{{I}}\right) \\ $$$$\:\:\:\mathrm{8}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\mathrm{8}{q}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\right)\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$+{q}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{25}{q}^{\mathrm{2}} }{\mathrm{9}}−\frac{\mathrm{40}\sqrt{\mathrm{2}}{q}}{\mathrm{3}\sqrt{\mathrm{3}}}+\frac{\mathrm{16}}{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{25}{q}^{\mathrm{2}} −\mathrm{40}\sqrt{\mathrm{6}}{q}+\mathrm{48}=\mathrm{0} \\ $$$${q}=\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{5}}−\frac{\sqrt{\mathrm{96}−\mathrm{48}}}{\mathrm{5}}\:=\:\frac{\mathrm{4}\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}\right)}{\mathrm{5}} \\ $$$${q}\:\approx\:\mathrm{0}.\mathrm{57395} \\ $$$$\mathrm{2}\bigtriangleup=\frac{\mathrm{2}{mq}−{q}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{\mathrm{4}{m}−{q}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)} \\ $$$$\:\bigtriangleup=\:\frac{\mathrm{4}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}}{\mathrm{5}}\right)\left\{\frac{\mathrm{2}\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}−\frac{\mathrm{20}}{\mathrm{3}}\left(\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}}{\mathrm{5}}\right)}{\mathrm{4}\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}−\frac{\mathrm{20}}{\mathrm{3}}\left(\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}}{\mathrm{5}}\right)}\right\} \\ $$$$\:=\:\frac{\mathrm{2}\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}\right)}{\mathrm{5}}\left(\frac{\mathrm{2}\sqrt{\mathrm{6}}−\mathrm{4}\sqrt{\mathrm{6}}+\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{4}\sqrt{\mathrm{6}}−\mathrm{4}\sqrt{\mathrm{6}}+\mathrm{4}\sqrt{\mathrm{3}}}\right) \\ $$$$\:=\:\frac{\mathrm{2}\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}\right)}{\mathrm{5}}\left(\frac{\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{4}\sqrt{\mathrm{3}}}\right) \\ $$$$\:=\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}}\right)}{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\bigtriangleup\:=\:\frac{\sqrt{\mathrm{6}}}{\mathrm{5}}\:\:{sq}.\:{units}\:\:\:\bigstar \\ $$$$\:\bigtriangleup\approx\:\mathrm{0}.\mathrm{489897949} \\ $$$$\%\:{shaded}\:{area}\:=\:\frac{\mathrm{40}\sqrt{\mathrm{6}}}{\pi}\:\approx\:\mathrm{31}.\mathrm{187872} \\ $$
Commented by mr W last updated on 26/Nov/20
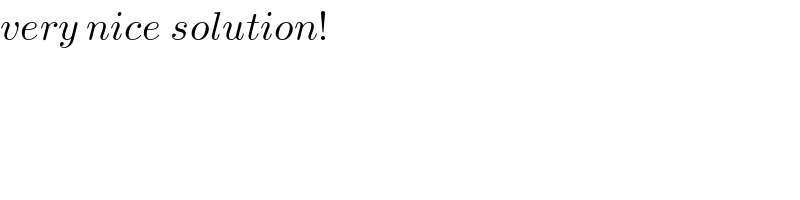
$${very}\:{nice}\:{solution}! \\ $$
