Question Number 123577 by bramlexs22 last updated on 26/Nov/20

Answered by Olaf last updated on 26/Nov/20
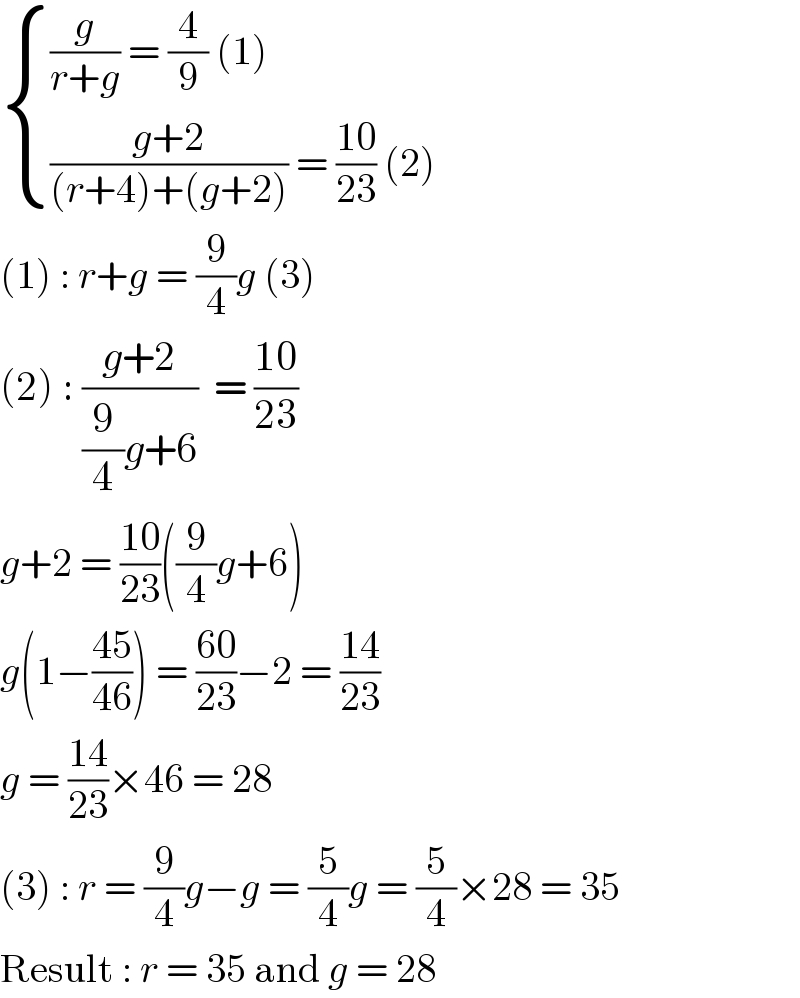
$$\begin{cases}{\frac{{g}}{{r}+{g}}\:=\:\frac{\mathrm{4}}{\mathrm{9}}\:\left(\mathrm{1}\right)}\\{\frac{{g}+\mathrm{2}}{\left({r}+\mathrm{4}\right)+\left({g}+\mathrm{2}\right)}\:=\:\frac{\mathrm{10}}{\mathrm{23}}\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\left(\mathrm{1}\right)\::\:{r}+{g}\:=\:\frac{\mathrm{9}}{\mathrm{4}}{g}\:\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right)\::\:\frac{{g}+\mathrm{2}}{\frac{\mathrm{9}}{\mathrm{4}}{g}+\mathrm{6}}\:\:=\:\frac{\mathrm{10}}{\mathrm{23}} \\ $$$${g}+\mathrm{2}\:=\:\frac{\mathrm{10}}{\mathrm{23}}\left(\frac{\mathrm{9}}{\mathrm{4}}{g}+\mathrm{6}\right) \\ $$$${g}\left(\mathrm{1}−\frac{\mathrm{45}}{\mathrm{46}}\right)\:=\:\frac{\mathrm{60}}{\mathrm{23}}−\mathrm{2}\:=\:\frac{\mathrm{14}}{\mathrm{23}} \\ $$$${g}\:=\:\frac{\mathrm{14}}{\mathrm{23}}×\mathrm{46}\:=\:\mathrm{28} \\ $$$$\left(\mathrm{3}\right)\::\:{r}\:=\:\frac{\mathrm{9}}{\mathrm{4}}{g}−{g}\:=\:\frac{\mathrm{5}}{\mathrm{4}}{g}\:=\:\frac{\mathrm{5}}{\mathrm{4}}×\mathrm{28}\:=\:\mathrm{35} \\ $$$$\mathrm{Result}\::\:{r}\:=\:\mathrm{35}\:\mathrm{and}\:{g}\:=\:\mathrm{28} \\ $$
