Question Number 123591 by ajfour last updated on 26/Nov/20
Commented by ajfour last updated on 26/Nov/20
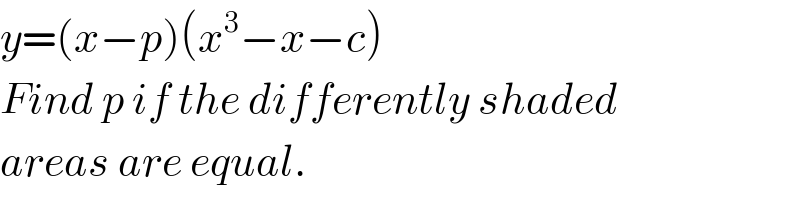
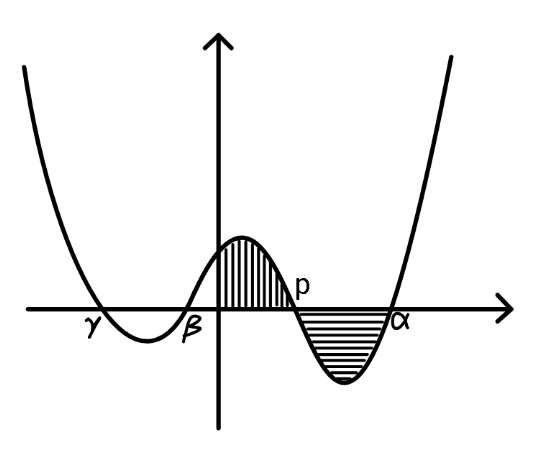
$${y}=\left({x}−{p}\right)\left({x}^{\mathrm{3}} −{x}−{c}\right) \\ $$$${Find}\:{p}\:{if}\:{the}\:{differently}\:{shaded} \\ $$$${areas}\:{are}\:{equal}. \\ $$
Commented by MJS_new last updated on 26/Nov/20

$$\mathrm{my}\:\mathrm{try}: \\ $$$$\mathrm{choose}\:{v},\:{w}\:>\mathrm{0}\:\mathrm{and}\:\mathrm{let} \\ $$$$\alpha=\frac{{v}+{w}}{\:\sqrt{{v}^{\mathrm{2}} +{vw}+{w}^{\mathrm{2}} }}\wedge\beta=−\frac{{v}}{\:\sqrt{{v}^{\mathrm{2}} +{vw}+{w}^{\mathrm{2}} }}\wedge\gamma=−\frac{{w}}{\:\sqrt{{v}^{\mathrm{2}} +{vw}+{w}^{\mathrm{2}} }} \\ $$$$\Rightarrow \\ $$$$\left({x}−\alpha\right)\left({x}−\beta\right)\left({x}−\gamma\right)= \\ $$$$={x}^{\mathrm{3}} −{x}−{c}\:\wedge\:{c}=\frac{{v}\left({v}+{w}\right){w}}{\left({v}^{\mathrm{2}} +{vw}+{w}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{{p}} {\int}}\left({x}−{p}\right)\left({x}^{\mathrm{3}} −{x}−{c}\right){dx}+\underset{{p}} {\overset{\alpha} {\int}}\left({x}−{p}\right)\left({x}^{\mathrm{3}} −{x}−{c}\right){dx}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${p}=\frac{\mathrm{2}\left(\mathrm{15}{c}−\mathrm{2}\alpha\left(\mathrm{3}\alpha^{\mathrm{2}} −\mathrm{5}\right)\right)\alpha}{\mathrm{15}\left(\mathrm{4}{c}−\alpha\left(\alpha^{\mathrm{2}} −\mathrm{2}\right)\right)}= \\ $$$$=\frac{\mathrm{2}\left({v}+{w}\right)\left(\mathrm{4}{v}^{\mathrm{2}} +\mathrm{13}{vw}+\mathrm{4}{w}^{\mathrm{2}} \right)}{\left({v}^{\mathrm{2}} +\mathrm{4}{vw}+{w}^{\mathrm{2}} \right)\sqrt{{v}^{\mathrm{2}} +{vw}+{w}^{\mathrm{2}} }} \\ $$$$…\mathrm{did}\:\mathrm{the}\:{v}−{w}−\mathrm{thing}\:\mathrm{to}\:\mathrm{make}\:\mathrm{sure}\:\mathrm{it}\:\mathrm{looks} \\ $$$$\mathrm{like}\:\mathrm{your}\:\mathrm{graphic}… \\ $$
