Question Number 123697 by ajfour last updated on 27/Nov/20

Commented by ajfour last updated on 27/Nov/20
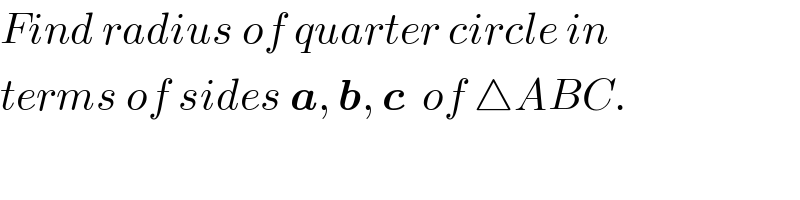
$${Find}\:{radius}\:{of}\:{quarter}\:{circle}\:{in} \\ $$$${terms}\:{of}\:{sides}\:\boldsymbol{{a}},\:\boldsymbol{{b}},\:\boldsymbol{{c}}\:\:{of}\:\bigtriangleup{ABC}. \\ $$
Answered by mr W last updated on 27/Nov/20

Commented by mr W last updated on 27/Nov/20
![B(0,0) A(c cos β,c sin β) C(a,0) x_D =(R/(tan β)) eqn. of AC: (y/(x−a))=((c sin β)/(c cos β−a)) c sin β x+(a−c cos β)y−ac sin β=0 R^2 =(([c sin β (R/(tan β))−ac sin β]^2 )/(c^2 sin^2 β+(a−c cos β)^2 )) R^2 =(((R cos β−a sin β)^2 c^2 )/(a^2 +c^2 −2ac cos β)) R^2 =(((R^2 cos^2 β+a^2 sin^2 β−aR sin 2β)c^2 )/b^2 ) (c^2 cos^2 β−b^2 )R^2 −ac^2 sin 2β R+a^2 c^2 sin^2 β=0 ⇒R=((ac sin β)/(c cos β+b)) =((2a^2 c sin β)/(a^2 +c^2 −b^2 +2ab)) R=((4aΔ)/(a^2 +c^2 −b^2 +2ab)) with Δ=(√(s(s−a)(s−b)(s−c))) example: c=a, b=(√2)a Δ=(a^2 /2) ⇒R=((4a×(a^2 /2))/(2(√2)a))=(a/( (√2))) ✓](https://www.tinkutara.com/question/Q123722.png)
$${B}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${A}\left({c}\:\mathrm{cos}\:\beta,{c}\:\mathrm{sin}\:\beta\right) \\ $$$${C}\left({a},\mathrm{0}\right) \\ $$$${x}_{{D}} =\frac{{R}}{\mathrm{tan}\:\beta} \\ $$$${eqn}.\:{of}\:{AC}: \\ $$$$\frac{{y}}{{x}−{a}}=\frac{{c}\:\mathrm{sin}\:\beta}{{c}\:\mathrm{cos}\:\beta−{a}} \\ $$$${c}\:\mathrm{sin}\:\beta\:{x}+\left({a}−{c}\:\mathrm{cos}\:\beta\right){y}−{ac}\:\mathrm{sin}\:\beta=\mathrm{0} \\ $$$${R}^{\mathrm{2}} =\frac{\left[{c}\:\mathrm{sin}\:\beta\:\frac{{R}}{\mathrm{tan}\:\beta}−{ac}\:\mathrm{sin}\:\beta\right]^{\mathrm{2}} }{{c}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\beta+\left({a}−{c}\:\mathrm{cos}\:\beta\right)^{\mathrm{2}} } \\ $$$${R}^{\mathrm{2}} =\frac{\left({R}\:\mathrm{cos}\:\beta−{a}\:\mathrm{sin}\:\beta\right)^{\mathrm{2}} {c}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}\:\mathrm{cos}\:\beta} \\ $$$${R}^{\mathrm{2}} =\frac{\left({R}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\beta+{a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\beta−{aR}\:\mathrm{sin}\:\mathrm{2}\beta\right){c}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\left({c}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\beta−{b}^{\mathrm{2}} \right){R}^{\mathrm{2}} −{ac}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\beta\:{R}+{a}^{\mathrm{2}} {c}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\beta=\mathrm{0} \\ $$$$\Rightarrow{R}=\frac{{ac}\:\mathrm{sin}\:\beta}{{c}\:\mathrm{cos}\:\beta+{b}} \\ $$$$=\frac{\mathrm{2}{a}^{\mathrm{2}} {c}\:\mathrm{sin}\:\beta}{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{2}{ab}} \\ $$$${R}=\frac{\mathrm{4}{a}\Delta}{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{2}{ab}} \\ $$$${with}\:\Delta=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$$ \\ $$$${example}: \\ $$$${c}={a},\:{b}=\sqrt{\mathrm{2}}{a} \\ $$$$\Delta=\frac{{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow{R}=\frac{\mathrm{4}{a}×\frac{{a}^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}{a}}=\frac{{a}}{\:\sqrt{\mathrm{2}}}\:\checkmark \\ $$
Commented by ajfour last updated on 27/Nov/20
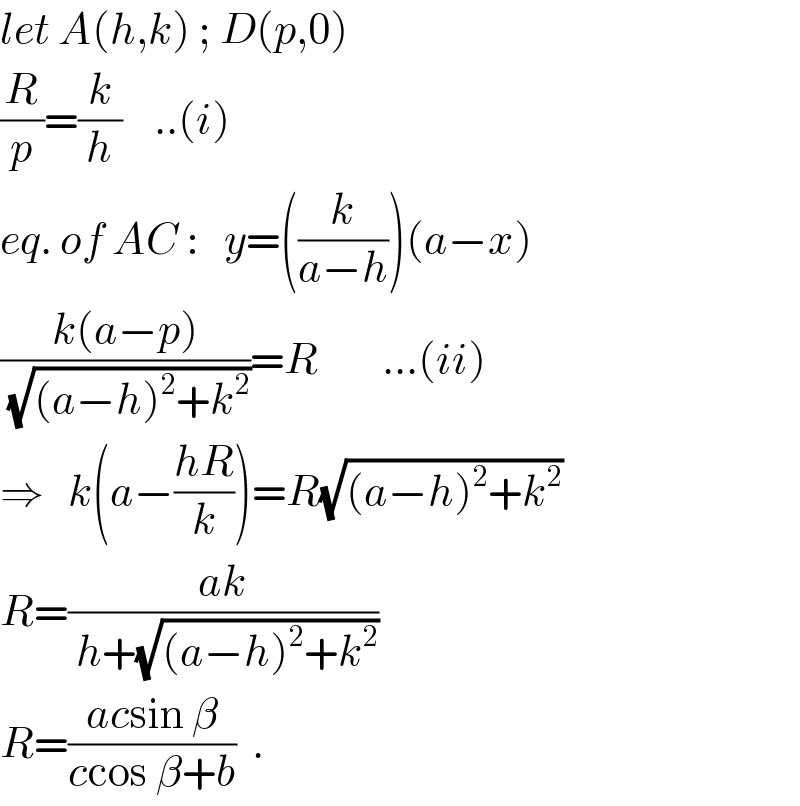
$${let}\:{A}\left({h},{k}\right)\:;\:{D}\left({p},\mathrm{0}\right) \\ $$$$\frac{{R}}{{p}}=\frac{{k}}{{h}}\:\:\:\:..\left({i}\right) \\ $$$${eq}.\:{of}\:{AC}\::\:\:\:{y}=\left(\frac{{k}}{{a}−{h}}\right)\left({a}−{x}\right) \\ $$$$\frac{{k}\left({a}−{p}\right)}{\:\sqrt{\left({a}−{h}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} }}={R}\:\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\:\:\:{k}\left({a}−\frac{{hR}}{{k}}\right)={R}\sqrt{\left({a}−{h}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} } \\ $$$${R}=\frac{{ak}}{\:{h}+\sqrt{\left({a}−{h}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} }} \\ $$$${R}=\frac{{ac}\mathrm{sin}\:\beta}{{c}\mathrm{cos}\:\beta+{b}}\:\:. \\ $$
Commented by ajfour last updated on 27/Nov/20
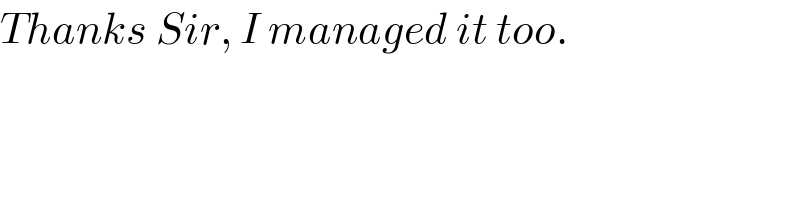
$${Thanks}\:{Sir},\:{I}\:{managed}\:{it}\:{too}. \\ $$
Commented by mr W last updated on 27/Nov/20

$${very}\:{nice}! \\ $$
