Question Number 123703 by Algoritm last updated on 27/Nov/20
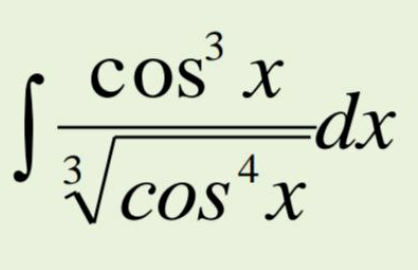
Answered by MJS_new last updated on 27/Nov/20
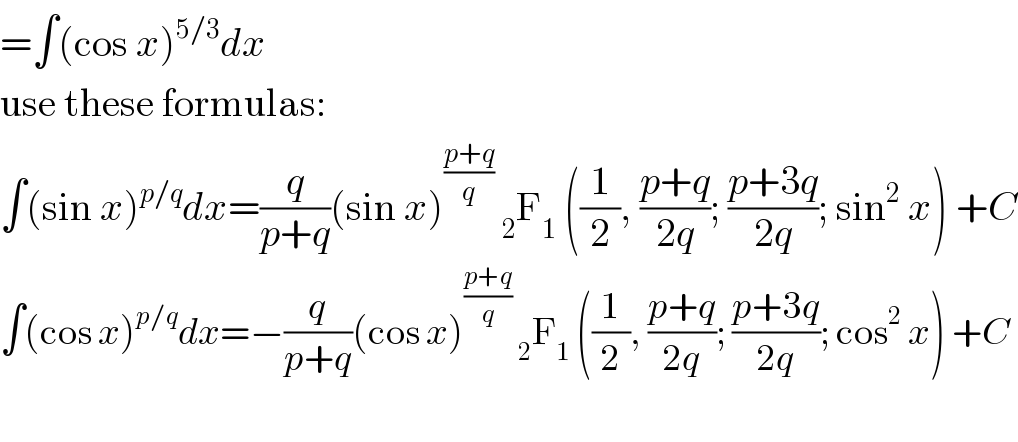
$$=\int\left(\mathrm{cos}\:{x}\right)^{\mathrm{5}/\mathrm{3}} {dx} \\ $$$$\mathrm{use}\:\mathrm{these}\:\mathrm{formulas}: \\ $$$$\int\left(\mathrm{sin}\:{x}\right)^{{p}/{q}} {dx}=\frac{{q}}{{p}+{q}}\left(\mathrm{sin}\:{x}\right)^{\frac{{p}+{q}}{{q}}} \:_{\mathrm{2}} \mathrm{F}_{\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{2}},\:\frac{{p}+{q}}{\mathrm{2}{q}};\:\frac{{p}+\mathrm{3}{q}}{\mathrm{2}{q}};\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)\:+{C} \\ $$$$\int\left(\mathrm{cos}\:{x}\right)^{{p}/{q}} {dx}=−\frac{{q}}{{p}+{q}}\left(\mathrm{cos}\:{x}\right)^{\frac{{p}+{q}}{{q}}} \:_{\mathrm{2}} \mathrm{F}_{\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{2}},\:\frac{{p}+{q}}{\mathrm{2}{q}};\:\frac{{p}+\mathrm{3}{q}}{\mathrm{2}{q}};\:\mathrm{cos}^{\mathrm{2}} \:{x}\right)\:+{C} \\ $$$$ \\ $$
