Question Number 123708 by mnjuly1970 last updated on 27/Nov/20

Commented by mnjuly1970 last updated on 27/Nov/20

$${please}\:{prove}\:\Uparrow\Uparrow \\ $$
Answered by ajfour last updated on 27/Nov/20
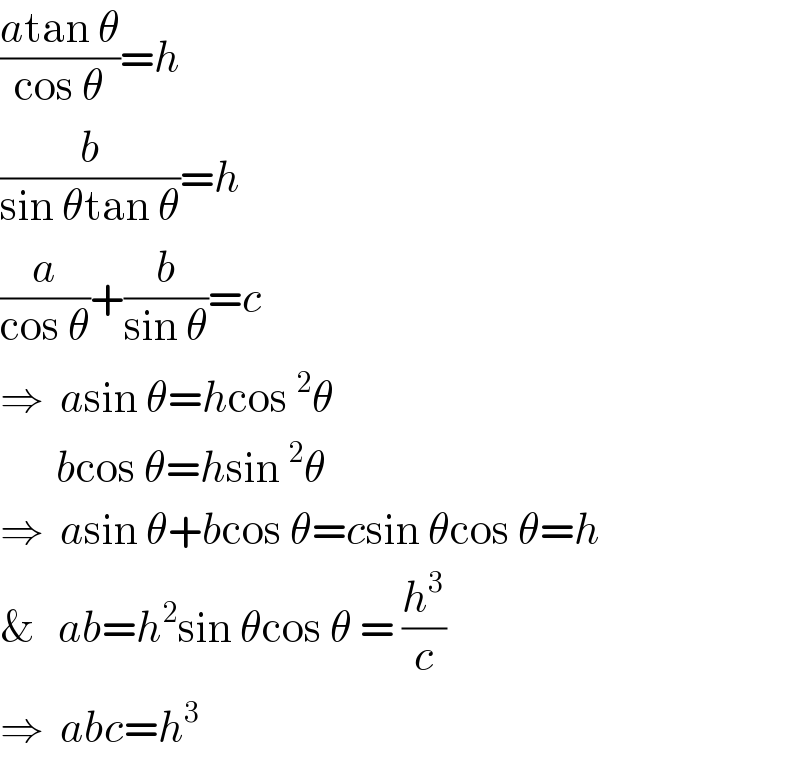
$$\frac{{a}\mathrm{tan}\:\theta}{\mathrm{cos}\:\theta}={h} \\ $$$$\frac{{b}}{\mathrm{sin}\:\theta\mathrm{tan}\:\theta}={h} \\ $$$$\frac{{a}}{\mathrm{cos}\:\theta}+\frac{{b}}{\mathrm{sin}\:\theta}={c} \\ $$$$\Rightarrow\:\:{a}\mathrm{sin}\:\theta={h}\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:\:\:{b}\mathrm{cos}\:\theta={h}\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\:\:{a}\mathrm{sin}\:\theta+{b}\mathrm{cos}\:\theta={c}\mathrm{sin}\:\theta\mathrm{cos}\:\theta={h} \\ $$$$\&\:\:\:{ab}={h}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta\:=\:\frac{{h}^{\mathrm{3}} }{{c}} \\ $$$$\Rightarrow\:\:{abc}={h}^{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 27/Nov/20

$${bravo}\:\:{bravo}\:\:{master}\:\:{ajfor}. \\ $$$${thank}\:{you}\: \\ $$$$ \\ $$
Answered by ajfour last updated on 27/Nov/20

$${h}^{\mathrm{2}} =\left(\frac{{a}}{\mathrm{cos}\:\theta}\right)\left(\frac{{b}}{\mathrm{sin}\:\theta}\right)\:\:\:…\left({i}\right) \\ $$$${h}\left(\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}+\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}\right)={c}\:\:\:\: \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta\mathrm{cos}\:\theta=\frac{{h}}{{c}}\:\:\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right)\:\:\Rightarrow\:\:{h}^{\mathrm{3}} ={abc}\:. \\ $$
Commented by mnjuly1970 last updated on 27/Nov/20

$$\:{god}\:{keep}\:\:{you}\:\:{young}\:{master} \\ $$$$\:\:''\:{mr}\:\:{ajfor}\:''.. \\ $$
Commented by ajfour last updated on 27/Nov/20

$${thanks},\:{I}\:{wish}\:{the}\:{same}\:{for}\:{you}. \\ $$
