Question Number 123771 by benjo_mathlover last updated on 28/Nov/20

Commented by benjo_mathlover last updated on 28/Nov/20
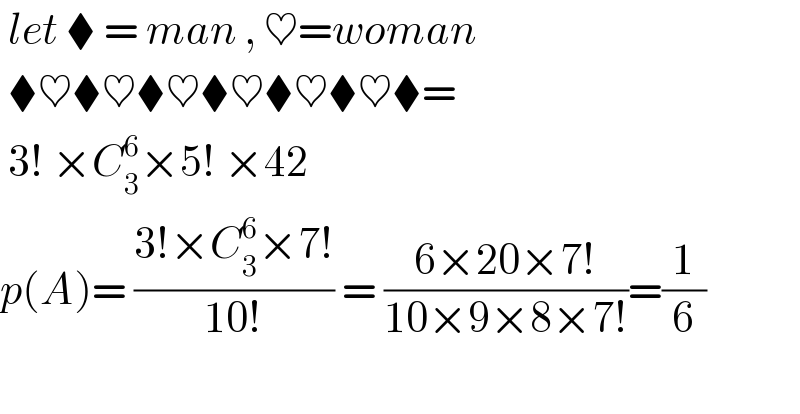
$$\:{let}\:\blacklozenge\:=\:{man}\:,\:\heartsuit={woman} \\ $$$$\:\blacklozenge\heartsuit\blacklozenge\heartsuit\blacklozenge\heartsuit\blacklozenge\heartsuit\blacklozenge\heartsuit\blacklozenge\heartsuit\blacklozenge= \\ $$$$\:\mathrm{3}!\:×{C}_{\mathrm{3}} ^{\mathrm{6}} ×\mathrm{5}!\:×\mathrm{42} \\ $$$${p}\left({A}\right)=\:\frac{\mathrm{3}!×{C}_{\mathrm{3}} ^{\mathrm{6}} ×\mathrm{7}!}{\mathrm{10}!}\:=\:\frac{\mathrm{6}×\mathrm{20}×\mathrm{7}!}{\mathrm{10}×\mathrm{9}×\mathrm{8}×\mathrm{7}!}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\: \\ $$
Commented by benjo_mathlover last updated on 28/Nov/20

$${it}\:{is}\:{correct}\:? \\ $$
Commented by mr W last updated on 28/Nov/20
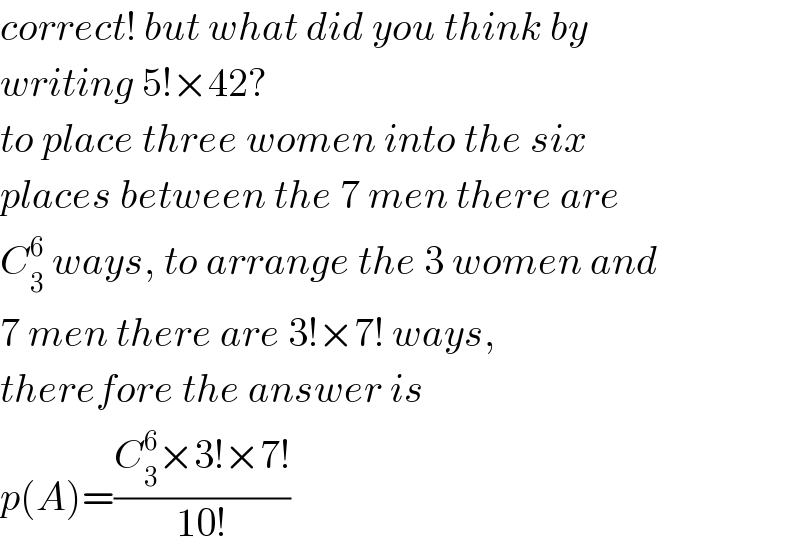
$${correct}!\:{but}\:{what}\:{did}\:{you}\:{think}\:{by} \\ $$$${writing}\:\mathrm{5}!×\mathrm{42}? \\ $$$${to}\:{place}\:{three}\:{women}\:{into}\:{the}\:{six}\: \\ $$$${places}\:{between}\:{the}\:\mathrm{7}\:{men}\:{there}\:{are} \\ $$$${C}_{\mathrm{3}} ^{\mathrm{6}} \:{ways},\:{to}\:{arrange}\:{the}\:\mathrm{3}\:{women}\:{and} \\ $$$$\mathrm{7}\:{men}\:{there}\:{are}\:\mathrm{3}!×\mathrm{7}!\:{ways},\: \\ $$$${therefore}\:{the}\:{answer}\:{is} \\ $$$${p}\left({A}\right)=\frac{{C}_{\mathrm{3}} ^{\mathrm{6}} ×\mathrm{3}!×\mathrm{7}!}{\mathrm{10}!} \\ $$
Commented by benjo_mathlover last updated on 28/Nov/20
because at both ends have to be occupied by men then many ways 6x7 = 42 sir
Commented by mr W last updated on 28/Nov/20

$${but}\:{we}\:{don}'{t}\:{need}\:{to}\:{arrange}\:{the}\:{two} \\ $$$${men}\:{at}\:{ends}\:{at}\:{first}\:{and}\:{then}\:{the} \\ $$$${other}\:{five}\:{men},\:{we}\:{can}\:{arrange}\:{all} \\ $$$$\mathrm{7}\:{men}\:{all}\:{at}\:{once}.\:{certainly}\:{the} \\ $$$${result}\:{is}\:{the}\:{same}: \\ $$$$\mathrm{7}×\mathrm{6}×\mathrm{5}!=\mathrm{7}! \\ $$
Commented by benjo_mathlover last updated on 28/Nov/20
$${oo}\:{thank}\:{you}\:{sir} \\ $$
