Question Number 123799 by benjo_mathlover last updated on 28/Nov/20
Commented by benjo_mathlover last updated on 28/Nov/20

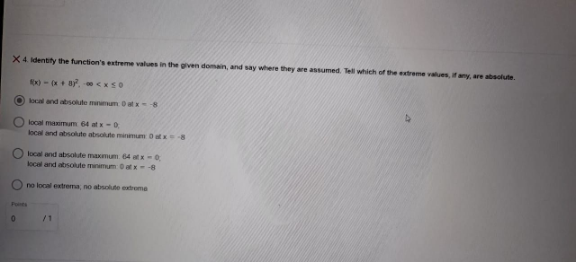
$${Identify}\:{the}\:{functions}\:{extreme} \\ $$$${values}\:{in}\:{given}\:{domain}\:{and}\: \\ $$$${say}\:{where}\:{they}\:{are}\:{assumed}\:. \\ $$$${Tell}\:{which}\:{of}\:{extreme}\:{values} \\ $$$${if}\:{any}\:{are}\:{absolute}\: \\ $$$${f}\left({x}\right)=\left({x}+\mathrm{8}\right)^{\mathrm{2}} \:;−\infty<{x}\leqslant\mathrm{0} \\ $$$$\left({a}\right)\:{local}\:{and}\:{absolute}\:{minimum}\:\mathrm{0}\:{at}\:{x}=−\mathrm{8} \\ $$$$\left({b}\right)\:{local}\:{maximum}\:\mathrm{64}\:{at}\:{x}=\mathrm{0} \\ $$$$\:\:\:\:\:\:{local}\:{and}\:{absolute}\:{minimum}\:\mathrm{0}\:{at}\:{x}=−\mathrm{8} \\ $$$$\left({c}\right)\:{local}\:{and}\:{absolute}\:{maximum}\:\mathrm{64}\:{at}\:{x}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{local}\:{and}\:{absolute}\:{minimum}\:\mathrm{0}\:{at}\:{x}=−\mathrm{8} \\ $$$$\left({d}\right)\:{no}\:{local}\:{extrema},\:{no}\:{absolute}\:{extrema} \\ $$
Commented by benjo_mathlover last updated on 28/Nov/20

$${look}\:{above}\:{sir} \\ $$
Answered by liberty last updated on 28/Nov/20
![find derivative f ′(x): f ′(x)=2(x+8) it vanishes at one point x_1 =−8 lie inside the indicated interval (−∞,0 ] . To find the extreme values of the function it is necessary to compute its value at the point x_1 =−8 and also at the end−point of the segment . f(−8)= 0 , f(0) = 64 and lim_(x→−∞) f(x) = +∞ it follows that absolute minimum 0 at x=−8 but no absolute maximum.](https://www.tinkutara.com/question/Q123808.png)
$${find}\:{derivative}\:{f}\:'\left({x}\right):\:{f}\:'\left({x}\right)=\mathrm{2}\left({x}+\mathrm{8}\right) \\ $$$${it}\:{vanishes}\:{at}\:{one}\:{point}\:{x}_{\mathrm{1}} =−\mathrm{8}\:{lie}\:{inside}\: \\ $$$${the}\:{indicated}\:{interval}\:\left(−\infty,\mathrm{0}\:\right]\:.\:{To}\:{find}\:{the}\: \\ $$$${extreme}\:{values}\:{of}\:{the}\:{function}\:{it}\:{is}\:{necessary} \\ $$$${to}\:{compute}\:{its}\:{value}\:{at}\:{the}\:{point}\:{x}_{\mathrm{1}} =−\mathrm{8}\:{and} \\ $$$${also}\:{at}\:{the}\:{end}−{point}\:{of}\:{the}\:{segment}\:. \\ $$$${f}\left(−\mathrm{8}\right)=\:\mathrm{0}\:,\:{f}\left(\mathrm{0}\right)\:=\:\mathrm{64}\:{and}\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}{f}\left({x}\right)\:=\:+\infty \\ $$$${it}\:{follows}\:{that}\:\:{absolute}\:{minimum}\:\mathrm{0}\:{at}\:{x}=−\mathrm{8} \\ $$$${but}\:{no}\:{absolute}\:{maximum}. \\ $$
