Question Number 123843 by mnjuly1970 last updated on 28/Nov/20

Commented by mnjuly1970 last updated on 28/Nov/20

$${please}\:{solve}\Uparrow\Uparrow \\ $$
Answered by mr W last updated on 28/Nov/20
Commented by mr W last updated on 28/Nov/20

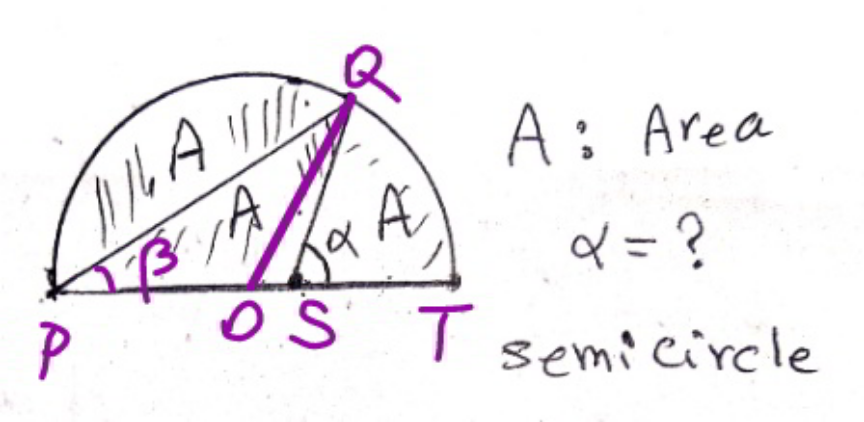
$${say}\:{radius}={R} \\ $$$${area}\:{of}\:{segment}=\frac{{semicircle}}{\mathrm{3}}=\frac{{circle}}{\mathrm{6}} \\ $$$$\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\pi−\mathrm{2}\beta−\mathrm{sin}\:\mathrm{2}\beta\right)=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\mathrm{2}\beta+\mathrm{sin}\:\mathrm{2}\beta=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow\beta=\mathrm{0}.\mathrm{5863}\left(=\mathrm{33}.\mathrm{6}°\right) \\ $$$$ \\ $$$${PQ}=\mathrm{2}{R}\:\mathrm{cos}\:\beta \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}{R}\:\mathrm{cos}\:\beta×{PS}×\mathrm{sin}\:\beta=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\Rightarrow{PS}=\frac{\pi{R}}{\mathrm{3}\:\mathrm{sin}\:\mathrm{2}\beta} \\ $$$$\frac{\mathrm{sin}\:\left(\alpha−\beta\right)}{\mathrm{sin}\:\alpha}=\frac{{PS}}{{PQ}}=\frac{\pi{R}}{\mathrm{3}\:\mathrm{sin}\:\mathrm{2}\beta×\mathrm{2}{R}\:\mathrm{cos}\:\beta} \\ $$$$\mathrm{cos}\:\beta−\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\alpha}=\frac{\pi}{\mathrm{6}\:\mathrm{sin}\:\mathrm{2}\beta\:\:\mathrm{cos}\:\beta} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{sin}\:\beta}{\mathrm{cos}\:\beta−\frac{\pi}{\mathrm{6}\:\mathrm{sin}\:\mathrm{2}\beta\:\:\mathrm{cos}\:\beta}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{sin}\:\mathrm{2}\beta}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta−\frac{\pi}{\mathrm{3}\:\mathrm{sin}\:\mathrm{2}\beta}} \\ $$$$\alpha=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\mathrm{2}\beta}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta−\frac{\pi}{\mathrm{3}\:\mathrm{sin}\:\mathrm{2}\beta}}\right)=\mathrm{74}.\mathrm{7}° \\ $$
Commented by mnjuly1970 last updated on 29/Nov/20

$${thank}\:{you}\:{so}\:{much} \\ $$$${master}\:\:{W}…. \\ $$
