Question Number 123894 by john_santu last updated on 29/Nov/20

Answered by mr W last updated on 29/Nov/20
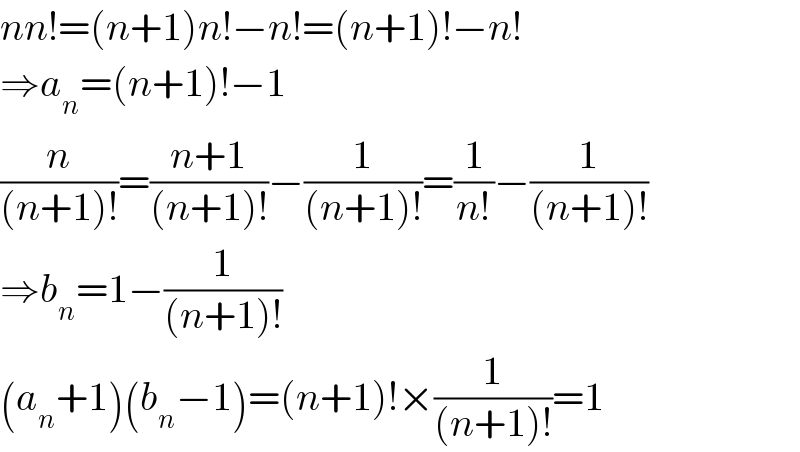
$${nn}!=\left({n}+\mathrm{1}\right){n}!−{n}!=\left({n}+\mathrm{1}\right)!−{n}! \\ $$$$\Rightarrow{a}_{{n}} =\left({n}+\mathrm{1}\right)!−\mathrm{1} \\ $$$$\frac{{n}}{\left({n}+\mathrm{1}\right)!}=\frac{{n}+\mathrm{1}}{\left({n}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}=\frac{\mathrm{1}}{{n}!}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\Rightarrow{b}_{{n}} =\mathrm{1}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\left({a}_{{n}} +\mathrm{1}\right)\left({b}_{{n}} −\mathrm{1}\right)=\left({n}+\mathrm{1}\right)!×\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}=\mathrm{1} \\ $$
Answered by mindispower last updated on 29/Nov/20
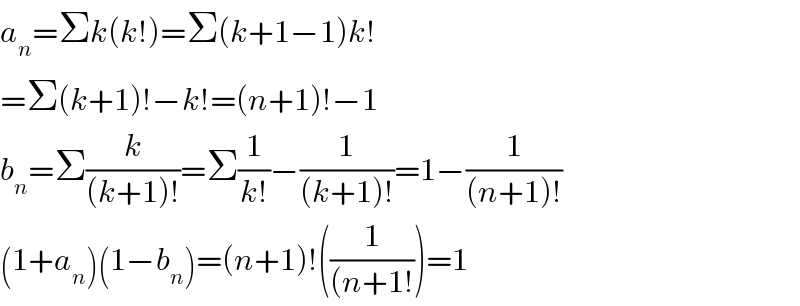
$${a}_{{n}} =\Sigma{k}\left({k}!\right)=\Sigma\left({k}+\mathrm{1}−\mathrm{1}\right){k}! \\ $$$$=\Sigma\left({k}+\mathrm{1}\right)!−{k}!=\left({n}+\mathrm{1}\right)!−\mathrm{1} \\ $$$${b}_{{n}} =\Sigma\frac{{k}}{\left({k}+\mathrm{1}\right)!}=\Sigma\frac{\mathrm{1}}{{k}!}−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)!}=\mathrm{1}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\left(\mathrm{1}+{a}_{{n}} \right)\left(\mathrm{1}−{b}_{{n}} \right)=\left({n}+\mathrm{1}\right)!\left(\frac{\mathrm{1}}{\left({n}+\mathrm{1}!\right.}\right)=\mathrm{1} \\ $$
