Question-124024

Question Number 124024 by hatakekakashi1729gmailcom last updated on 30/Nov/20

Answered by Dwaipayan Shikari last updated on 30/Nov/20

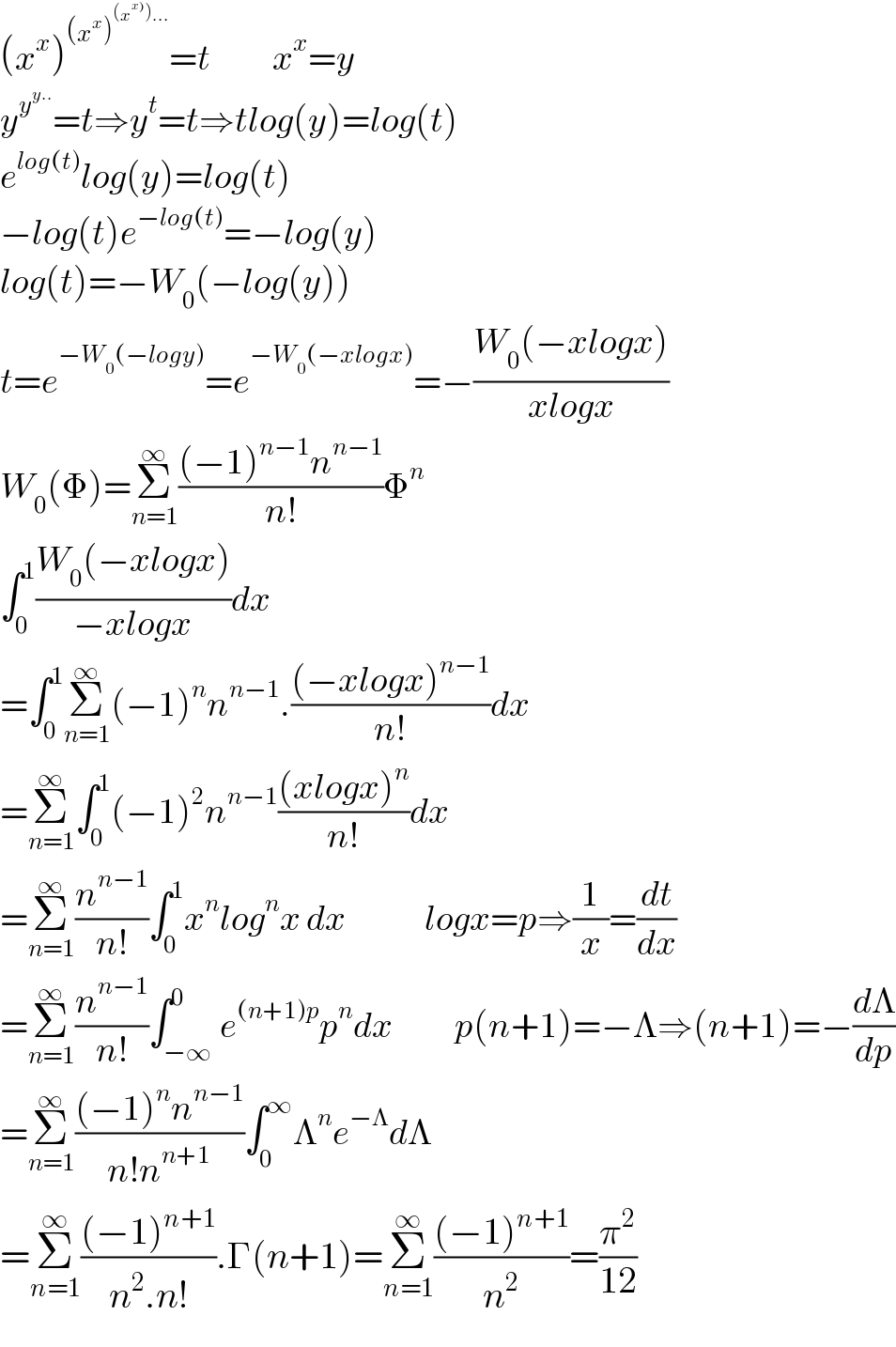
(x^x )^((x^x )^((x^(x)) )...) ) =t x^x =y y^y^(y..) =t⇒y^t =t⇒tlog(y)=log(t) e^(log(t)) log(y)=log(t) −log(t)e^(−log(t)) =−log(y) log(t)=−W_0 (−log(y)) t=e^(−W_0 (−logy)) =e^(−W_0 (−xlogx)) =−((W_0 (−xlogx))/(xlogx)) W_0 (Φ)=Σ_(n=1) ^∞ (((−1)^(n−1) n^(n−1) )/(n!))Φ^n ∫_0 ^1 ((W_0 (−xlogx))/(−xlogx))dx =∫_0 ^1 Σ_(n=1) ^∞ (−1)^n n^(n−1) .(((−xlogx)^(n−1) )/(n!))dx =Σ_(n=1) ^∞ ∫_0 ^1 (−1)^2 n^(n−1) (((xlogx)^n )/(n!))dx =Σ_(n=1) ^∞ (n^(n−1) /(n!))∫_0 ^1 x^n log^n x dx logx=p⇒(1/x)=(dt/dx) =Σ_(n=1) ^∞ (n^(n−1) /(n!))∫_(−∞) ^0 e^((n+1)p) p^n dx p(n+1)=−Λ⇒(n+1)=−(dΛ/dp) =Σ_(n=1) ^∞ (((−1)^n n^(n−1) )/(n!n^(n+1) ))∫_0 ^∞ Λ^n e^(−Λ) dΛ =Σ_(n=1) ^∞ (((−1)^(n+1) )/(n^2 .n!)).Γ(n+1)=Σ_(n=1) ^∞ (((−1)^(n+1) )/n^2 )=(π^2 /(12))

$$\left({x}^{{x}} \right)^{\left({x}^{{x}} \right)^{\left({x}^{\left.{x}\right)} \right)…} } ={t}\:\:\:\:\:\:\:\:\:\:\:{x}^{{x}} ={y} \\ $$$${y}^{{y}^{{y}..} } ={t}\Rightarrow{y}^{{t}} ={t}\Rightarrow{tlog}\left({y}\right)={log}\left({t}\right) \\ $$$${e}^{{log}\left({t}\right)} {log}\left({y}\right)={log}\left({t}\right) \\ $$$$−{log}\left({t}\right){e}^{−{log}\left({t}\right)} =−{log}\left({y}\right) \\ $$$${log}\left({t}\right)=−{W}_{\mathrm{0}} \left(−{log}\left({y}\right)\right) \\ $$$${t}={e}^{−{W}_{\mathrm{0}} \left(−{logy}\right)} ={e}^{−{W}_{\mathrm{0}} \left(−{xlogx}\right)} =−\frac{{W}_{\mathrm{0}} \left(−{xlogx}\right)}{{xlogx}} \\ $$$${W}_{\mathrm{0}} \left(\Phi\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {n}^{{n}−\mathrm{1}} }{{n}!}\Phi^{{n}} \: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{W}_{\mathrm{0}} \left(−{xlogx}\right)}{−{xlogx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {n}^{{n}−\mathrm{1}} .\frac{\left(−{xlogx}\right)^{{n}−\mathrm{1}} }{{n}!}{dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{\mathrm{2}} {n}^{{n}−\mathrm{1}} \frac{\left({xlogx}\right)^{{n}} }{{n}!}{dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{{n}−\mathrm{1}} }{{n}!}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {log}^{{n}} {x}\:{dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{logx}={p}\Rightarrow\frac{\mathrm{1}}{{x}}=\frac{{dt}}{{dx}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{{n}−\mathrm{1}} }{{n}!}\int_{−\infty} ^{\mathrm{0}} {e}^{\left({n}+\mathrm{1}\right){p}} {p}^{{n}} {dx}\:\:\:\:\:\:\:\:\:\:\:{p}\left({n}+\mathrm{1}\right)=−\Lambda\Rightarrow\left({n}+\mathrm{1}\right)=−\frac{{d}\Lambda}{{dp}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {n}^{{n}−\mathrm{1}} }{{n}!{n}^{{n}+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} \Lambda^{{n}} {e}^{−\Lambda} {d}\Lambda \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}^{\mathrm{2}} .{n}!}.\Gamma\left({n}+\mathrm{1}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Commented by hatakekakashi1729gmailcom last updated on 02/Dec/20

$${Thanks} \\ $$

Commented by hatakekakashi1729gmailcom last updated on 30/Nov/20

$${don}'{t}\:{mind}\:{do}\:{you}\:{have}\:{another}\:{method} \\ $$

Commented by Dwaipayan Shikari last updated on 30/Nov/20

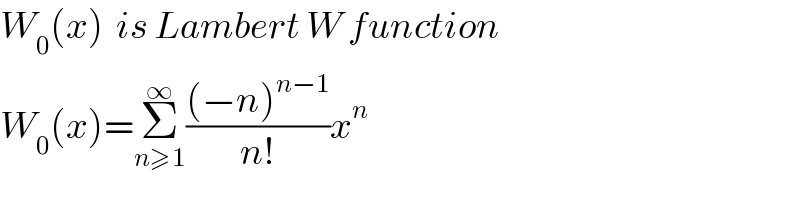
W_0 (x) is Lambert W function W_0 (x)=Σ_(n≥1) ^∞ (((−n)^(n−1) )/(n!))x^n

$${W}_{\mathrm{0}} \left({x}\right)\:\:{is}\:{Lambert}\:{W}\:{function} \\ $$$${W}_{\mathrm{0}} \left({x}\right)=\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}{x}^{{n}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply