Question Number 124099 by aurpeyz last updated on 30/Nov/20

Answered by liberty last updated on 30/Nov/20
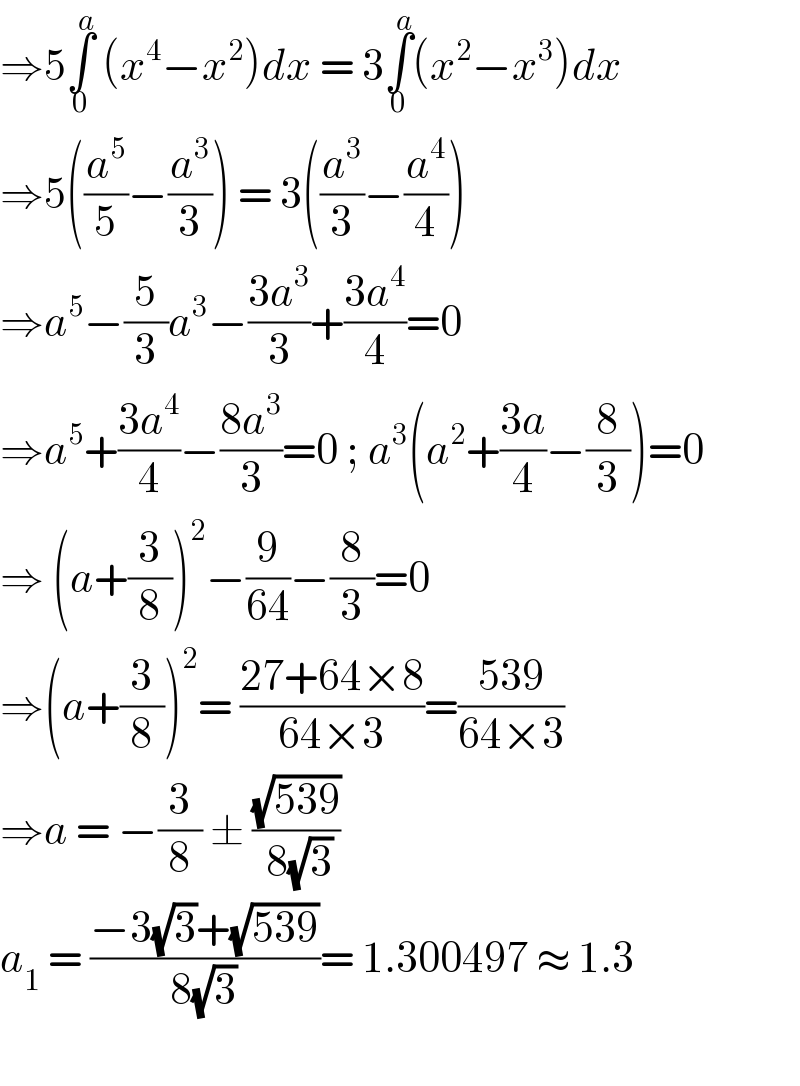
$$\Rightarrow\mathrm{5}\underset{\mathrm{0}} {\overset{{a}} {\int}}\:\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} \right){dx}\:=\:\mathrm{3}\underset{\mathrm{0}} {\overset{{a}} {\int}}\left({x}^{\mathrm{2}} −{x}^{\mathrm{3}} \right){dx} \\ $$$$\Rightarrow\mathrm{5}\left(\frac{{a}^{\mathrm{5}} }{\mathrm{5}}−\frac{{a}^{\mathrm{3}} }{\mathrm{3}}\right)\:=\:\mathrm{3}\left(\frac{{a}^{\mathrm{3}} }{\mathrm{3}}−\frac{{a}^{\mathrm{4}} }{\mathrm{4}}\right)\: \\ $$$$\Rightarrow{a}^{\mathrm{5}} −\frac{\mathrm{5}}{\mathrm{3}}{a}^{\mathrm{3}} −\frac{\mathrm{3}{a}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}{a}^{\mathrm{4}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{5}} +\frac{\mathrm{3}{a}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{8}{a}^{\mathrm{3}} }{\mathrm{3}}=\mathrm{0}\:;\:{a}^{\mathrm{3}} \left({a}^{\mathrm{2}} +\frac{\mathrm{3}{a}}{\mathrm{4}}−\frac{\mathrm{8}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\left({a}+\frac{\mathrm{3}}{\mathrm{8}}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{64}}−\frac{\mathrm{8}}{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\left({a}+\frac{\mathrm{3}}{\mathrm{8}}\right)^{\mathrm{2}} =\:\frac{\mathrm{27}+\mathrm{64}×\mathrm{8}}{\mathrm{64}×\mathrm{3}}=\frac{\mathrm{539}}{\mathrm{64}×\mathrm{3}} \\ $$$$\Rightarrow{a}\:=\:−\frac{\mathrm{3}}{\mathrm{8}}\:\pm\:\frac{\sqrt{\mathrm{539}}}{\:\mathrm{8}\sqrt{\mathrm{3}}} \\ $$$${a}_{\mathrm{1}} \:=\:\frac{−\mathrm{3}\sqrt{\mathrm{3}}+\sqrt{\mathrm{539}}}{\mathrm{8}\sqrt{\mathrm{3}}}=\:\mathrm{1}.\mathrm{300497}\:\approx\:\mathrm{1}.\mathrm{3} \\ $$$$ \\ $$
