Question Number 124141 by nico last updated on 01/Dec/20

Answered by Lordose last updated on 01/Dec/20
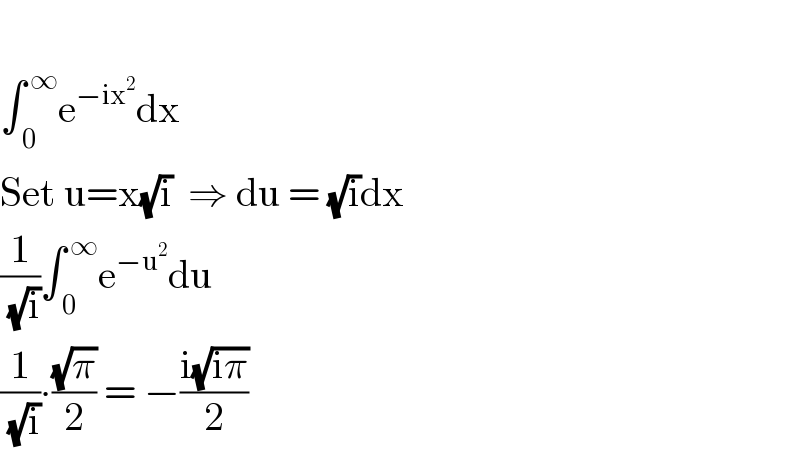
$$ \\ $$$$\int_{\:\mathrm{0}} ^{\:\infty} \mathrm{e}^{−\mathrm{ix}^{\mathrm{2}} } \mathrm{dx}\:\:\:\:\: \\ $$$$\mathrm{Set}\:\mathrm{u}=\mathrm{x}\sqrt{\mathrm{i}}\:\:\Rightarrow\:\mathrm{du}\:=\:\sqrt{\mathrm{i}}\mathrm{dx} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{i}}}\int_{\:\mathrm{0}} ^{\:\infty} \mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \mathrm{du} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{i}}}\centerdot\frac{\sqrt{\pi}}{\mathrm{2}}\:=\:−\frac{\mathrm{i}\sqrt{\mathrm{i}\pi}}{\mathrm{2}} \\ $$
Answered by Bird last updated on 01/Dec/20
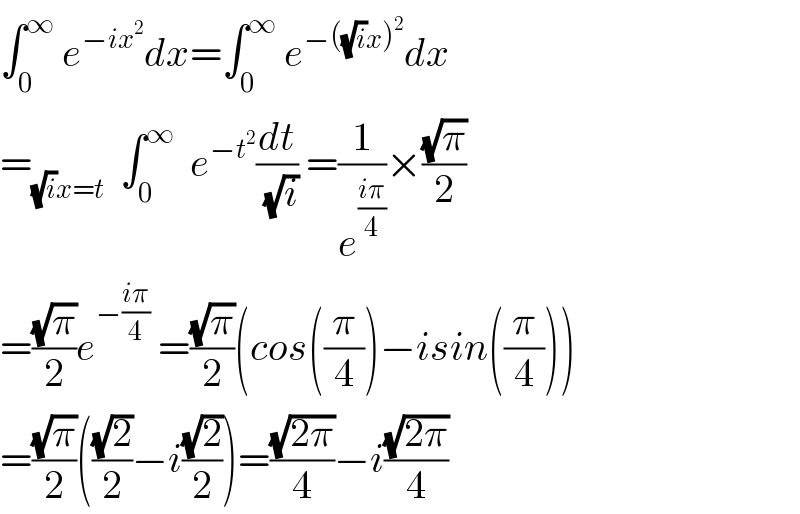
$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ix}^{\mathrm{2}} } {dx}=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left(\sqrt{{i}}{x}\right)^{\mathrm{2}} } {dx} \\ $$$$=_{\sqrt{{i}}{x}={t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{t}^{\mathrm{2}} } \frac{{dt}}{\:\sqrt{{i}}}\:=\frac{\mathrm{1}}{{e}^{\frac{{i}\pi}{\mathrm{4}}} }×\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:=\frac{\sqrt{\pi}}{\mathrm{2}}\left({cos}\left(\frac{\pi}{\mathrm{4}}\right)−{isin}\left(\frac{\pi}{\mathrm{4}}\right)\right) \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)=\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{4}}−{i}\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{4}} \\ $$
