Question Number 124173 by bramlexs22 last updated on 01/Dec/20
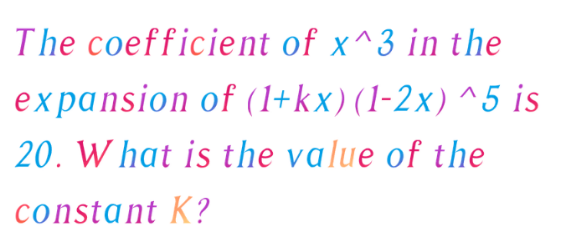
Answered by bobhans last updated on 01/Dec/20
![(1+kx)(1−2x)^5 = (1+kx)[Σ_(n=0) ^5 C_n ^( 5) (−2x)^(5−n) ] =(1+kx)(C_3 ^( 5) (−2x)^2 +C _2^5 (−2x)^3 ) =(1+kx)(80x^2 −160x^3 ) coefficient of x^3 ⇒80k−160=20 ⇒80k=180 ; k=((18)/8)= (9/4)](https://www.tinkutara.com/question/Q124174.png)
$$\left(\mathrm{1}+{kx}\right)\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{5}} \:=\:\left(\mathrm{1}+{kx}\right)\left[\underset{{n}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}{C}_{{n}} ^{\:\mathrm{5}} \left(−\mathrm{2}{x}\right)^{\mathrm{5}−{n}} \:\right] \\ $$$$=\left(\mathrm{1}+{kx}\right)\left({C}_{\mathrm{3}} ^{\:\mathrm{5}} \left(−\mathrm{2}{x}\right)^{\mathrm{2}} +{C}\:_{\mathrm{2}} ^{\mathrm{5}} \:\left(−\mathrm{2}{x}\right)^{\mathrm{3}} \right) \\ $$$$=\left(\mathrm{1}+{kx}\right)\left(\mathrm{80}{x}^{\mathrm{2}} −\mathrm{160}{x}^{\mathrm{3}} \right) \\ $$$${coefficient}\:{of}\:\:{x}^{\mathrm{3}} \:\Rightarrow\mathrm{80}{k}−\mathrm{160}=\mathrm{20} \\ $$$$\Rightarrow\mathrm{80}{k}=\mathrm{180}\:;\:{k}=\frac{\mathrm{18}}{\mathrm{8}}=\:\frac{\mathrm{9}}{\mathrm{4}} \\ $$
Commented by MJS_new last updated on 01/Dec/20

$$\mathrm{please}\:\mathrm{post}\:\mathrm{a}\:\mathrm{new}\:\mathrm{question}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{comments} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{easy},\:\mathrm{just}\:\mathrm{type}\:\mathrm{on}\:\mathrm{the}\:\equiv\:\mathrm{sign}\:\mathrm{in}\:\mathrm{the}\:\mathrm{left} \\ $$$$\mathrm{upper}\:\mathrm{corner},\:\mathrm{then}\:\mathrm{select}\:{forum}\:\mathrm{and}\:\mathrm{finally} \\ $$$$\mathrm{the}\:+\:\mathrm{on}\:\mathrm{top}. \\ $$
