Question Number 124189 by ajfour last updated on 01/Dec/20

Commented by ajfour last updated on 01/Dec/20
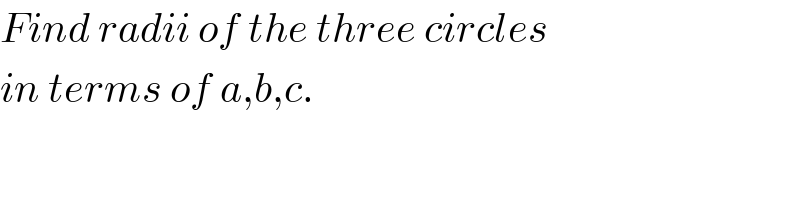
$${Find}\:{radii}\:{of}\:{the}\:{three}\:{circles} \\ $$$${in}\:{terms}\:{of}\:{a},{b},{c}. \\ $$
Commented by ajfour last updated on 01/Dec/20

$${thanks}\:{Sir}! \\ $$
Commented by mr W last updated on 01/Dec/20
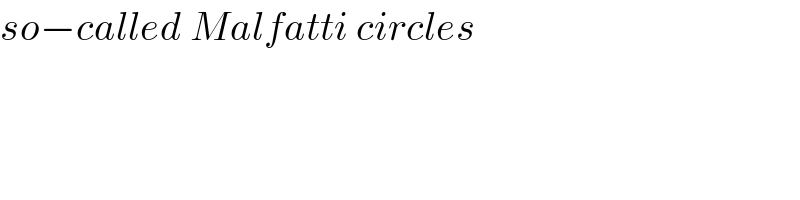
$${so}−{called}\:{Malfatti}\:{circles} \\ $$
Commented by mr W last updated on 01/Dec/20

Commented by MJS_new last updated on 01/Dec/20
![given a, b, c we can put the triangle as follows: A= ((0),(0) ) B= ((c),(0) ) C= ((((−a^2 +b^2 +c^2 )/(2c))),((δ/(2c))) ) the incenter is [M for mid−point to avoid another C] M_I = ((((−a+b+c)/2)),(r_I ) ) with r_I =(δ/(2(a+b+c))) the distances of this to the vertices are d=∣M_I A∣=(√(((−a+b+c)bc)/(a+b+c))) e=∣M_I B∣=(√((a(a−b+c)c)/(a+b+c))) f=∣M_I C∣=(√((a(a+b−c)c)/(a+b+c))) δ=(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) thought this might help](https://www.tinkutara.com/question/Q124236.png)
$$\mathrm{given}\:{a},\:{b},\:{c}\:\mathrm{we}\:\mathrm{can}\:\mathrm{put}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{as}\:\mathrm{follows}: \\ $$$${A}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{{c}}\\{\mathrm{0}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{c}}}\\{\frac{\delta}{\mathrm{2}{c}}}\end{pmatrix} \\ $$$$\mathrm{the}\:\mathrm{incenter}\:\mathrm{is}\:\left[{M}\:\mathrm{for}\:\mathrm{mid}−\mathrm{point}\:\mathrm{to}\:\mathrm{avoid}\right. \\ $$$$\left.\mathrm{another}\:{C}\right] \\ $$$${M}_{{I}} =\begin{pmatrix}{\frac{−{a}+{b}+{c}}{\mathrm{2}}}\\{{r}_{{I}} }\end{pmatrix}\:\:\mathrm{with}\:{r}_{{I}} =\frac{\delta}{\mathrm{2}\left({a}+{b}+{c}\right)} \\ $$$$\mathrm{the}\:\mathrm{distances}\:\mathrm{of}\:\mathrm{this}\:\mathrm{to}\:\mathrm{the}\:\mathrm{vertices}\:\mathrm{are} \\ $$$${d}=\mid{M}_{{I}} {A}\mid=\sqrt{\frac{\left(−{a}+{b}+{c}\right){bc}}{{a}+{b}+{c}}} \\ $$$${e}=\mid{M}_{{I}} {B}\mid=\sqrt{\frac{{a}\left({a}−{b}+{c}\right){c}}{{a}+{b}+{c}}} \\ $$$${f}=\mid{M}_{{I}} {C}\mid=\sqrt{\frac{{a}\left({a}+{b}−{c}\right){c}}{{a}+{b}+{c}}} \\ $$$$\delta=\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)} \\ $$$$\mathrm{thought}\:\mathrm{this}\:\mathrm{might}\:\mathrm{help} \\ $$
