Question-124191

Question Number 124191 by Algoritm last updated on 01/Dec/20

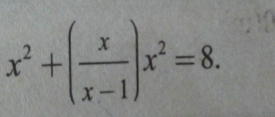
Answered by MJS_new last updated on 01/Dec/20

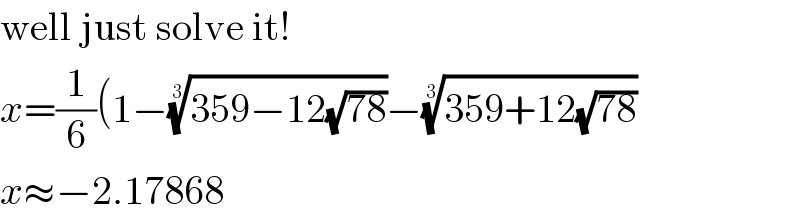
well just solve it! x=(1/6)(1−((359−12(√(78))))^(1/3) −((359+12(√(78))))^(1/3) x≈−2.17868

$$\mathrm{well}\:\mathrm{just}\:\mathrm{solve}\:\mathrm{it}! \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}−\sqrt[{\mathrm{3}}]{\mathrm{359}−\mathrm{12}\sqrt{\mathrm{78}}}−\sqrt[{\mathrm{3}}]{\mathrm{359}+\mathrm{12}\sqrt{\mathrm{78}}}\right. \\ $$$${x}\approx−\mathrm{2}.\mathrm{17868} \\ $$

Answered by Dwaipayan Shikari last updated on 01/Dec/20

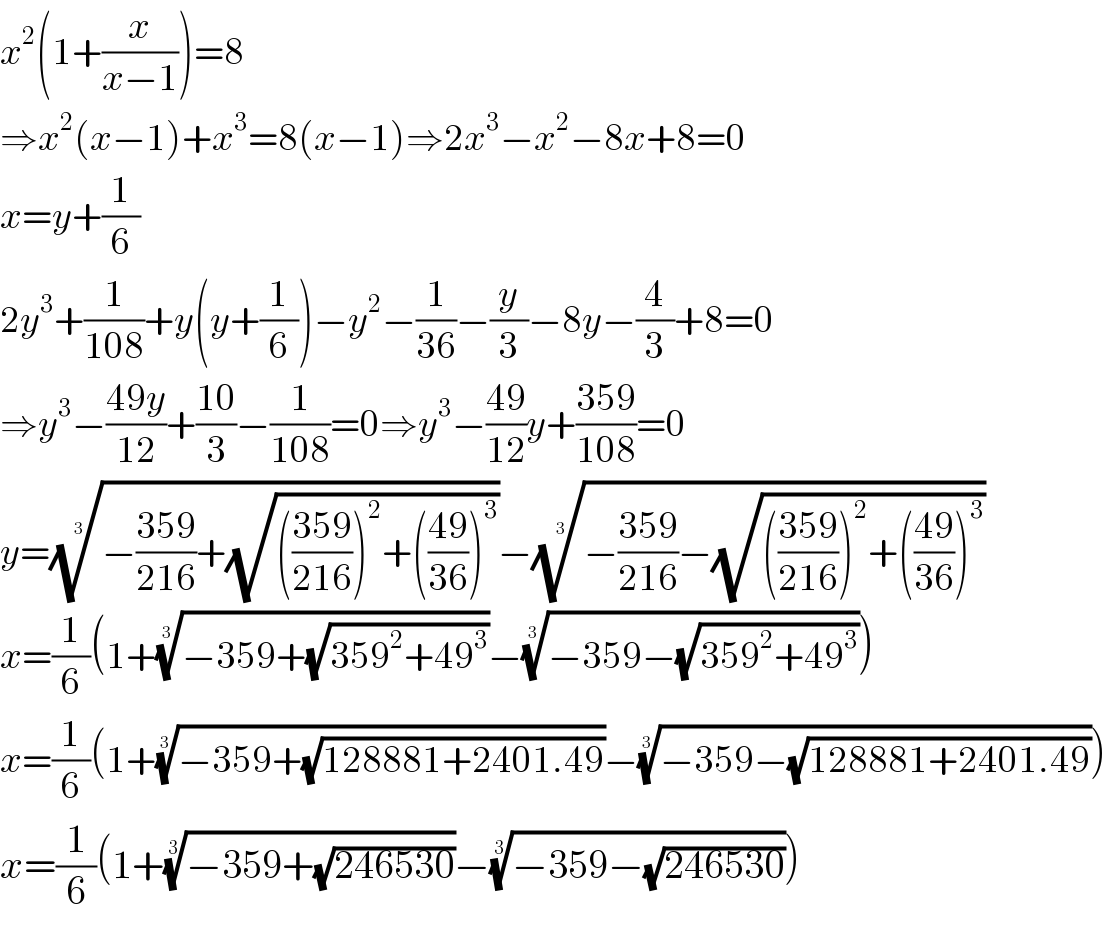
x^2 (1+(x/(x−1)))=8 ⇒x^2 (x−1)+x^3 =8(x−1)⇒2x^3 −x^2 −8x+8=0 x=y+(1/6) 2y^3 +(1/(108))+y(y+(1/6))−y^2 −(1/(36))−(y/3)−8y−(4/3)+8=0 ⇒y^3 −((49y)/(12))+((10)/3)−(1/(108))=0⇒y^3 −((49)/(12))y+((359)/(108))=0 y=((−((359)/(216))+(√((((359)/(216)))^2 +(((49)/(36)))^3 ))))^(1/3) −((−((359)/(216))−(√((((359)/(216)))^2 +(((49)/(36)))^3 ))))^(1/3) x=(1/6)(1+((−359+(√(359^2 +49^3 ))))^(1/3) −((−359−(√(359^2 +49^3 ))))^(1/3) ) x=(1/6)(1+((−359+(√(128881+2401.49))))^(1/3) −((−359−(√(128881+2401.49))))^(1/3) ) x=(1/6)(1+((−359+(√(246530))))^(1/3) −((−359−(√(246530))))^(1/3) )

$${x}^{\mathrm{2}} \left(\mathrm{1}+\frac{{x}}{{x}−\mathrm{1}}\right)=\mathrm{8} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)+{x}^{\mathrm{3}} =\mathrm{8}\left({x}−\mathrm{1}\right)\Rightarrow\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{8}=\mathrm{0} \\ $$$${x}={y}+\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{2}{y}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{108}}+{y}\left({y}+\frac{\mathrm{1}}{\mathrm{6}}\right)−{y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{36}}−\frac{{y}}{\mathrm{3}}−\mathrm{8}{y}−\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow{y}^{\mathrm{3}} −\frac{\mathrm{49}{y}}{\mathrm{12}}+\frac{\mathrm{10}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{108}}=\mathrm{0}\Rightarrow{y}^{\mathrm{3}} −\frac{\mathrm{49}}{\mathrm{12}}{y}+\frac{\mathrm{359}}{\mathrm{108}}=\mathrm{0} \\ $$$${y}=\sqrt[{\mathrm{3}}]{−\frac{\mathrm{359}}{\mathrm{216}}+\sqrt{\left(\frac{\mathrm{359}}{\mathrm{216}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{49}}{\mathrm{36}}\right)^{\mathrm{3}} }}−\sqrt[{\mathrm{3}}]{−\frac{\mathrm{359}}{\mathrm{216}}−\sqrt{\left(\frac{\mathrm{359}}{\mathrm{216}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{49}}{\mathrm{36}}\right)^{\mathrm{3}} }} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{−\mathrm{359}+\sqrt{\mathrm{359}^{\mathrm{2}} +\mathrm{49}^{\mathrm{3}} }}−\sqrt[{\mathrm{3}}]{−\mathrm{359}−\sqrt{\mathrm{359}^{\mathrm{2}} +\mathrm{49}^{\mathrm{3}} }}\right) \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{−\mathrm{359}+\sqrt{\mathrm{128881}+\mathrm{2401}.\mathrm{49}}}−\sqrt[{\mathrm{3}}]{−\mathrm{359}−\sqrt{\mathrm{128881}+\mathrm{2401}.\mathrm{49}}}\right) \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{−\mathrm{359}+\sqrt{\mathrm{246530}}}−\sqrt[{\mathrm{3}}]{−\mathrm{359}−\sqrt{\mathrm{246530}}}\right) \\ $$

Commented by Algoritm last updated on 01/Dec/20

$$\mathrm{thank}\:\mathrm{you} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply