Question Number 124264 by joki last updated on 02/Dec/20

Commented by bramlexs22 last updated on 02/Dec/20
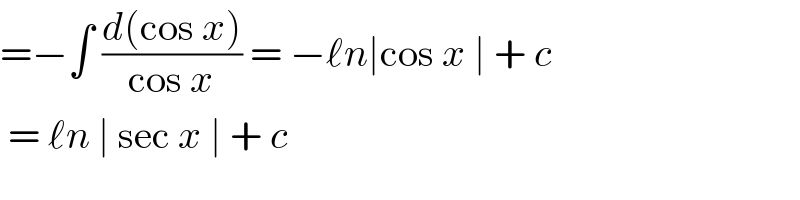
$$=−\int\:\frac{{d}\left(\mathrm{cos}\:{x}\right)}{\mathrm{cos}\:{x}}\:=\:−\ell{n}\mid\mathrm{cos}\:{x}\:\mid\:+\:{c} \\ $$$$\:=\:\ell{n}\:\mid\:\mathrm{sec}\:{x}\:\mid\:+\:{c}\: \\ $$
Commented by joki last updated on 02/Dec/20
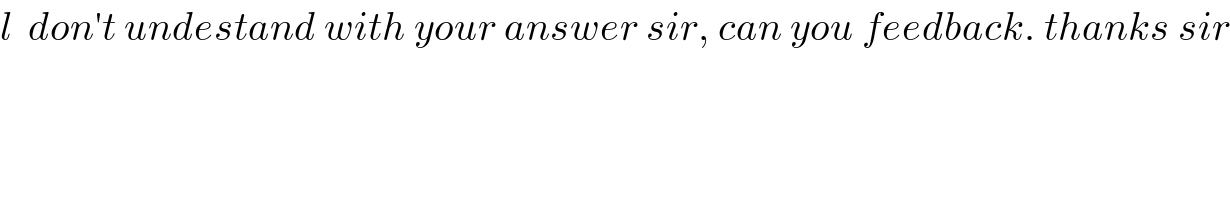
$${l}\:\:{don}'{t}\:{undestand}\:{with}\:{your}\:{answer}\:{sir},\:{can}\:{you}\:{feedback}.\:{thanks}\:{sir} \\ $$
Commented by bramlexs22 last updated on 02/Dec/20
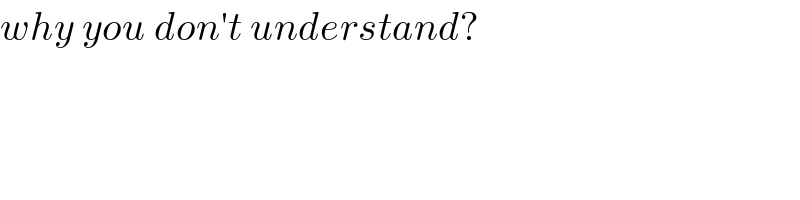
$${why}\:{you}\:{don}'{t}\:{understand}? \\ $$
Commented by Ar Brandon last updated on 02/Dec/20
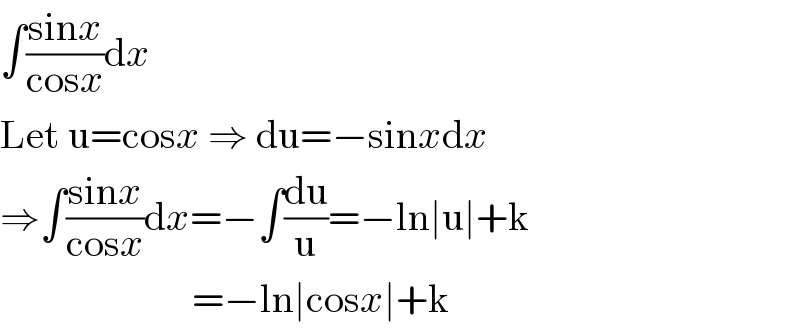
$$\int\frac{\mathrm{sin}{x}}{\mathrm{cos}{x}}\mathrm{d}{x} \\ $$$$\mathrm{Let}\:\mathrm{u}=\mathrm{cos}{x}\:\Rightarrow\:\mathrm{du}=−\mathrm{sin}{x}\mathrm{d}{x} \\ $$$$\Rightarrow\int\frac{\mathrm{sin}{x}}{\mathrm{cos}{x}}\mathrm{d}{x}=−\int\frac{\mathrm{du}}{\mathrm{u}}=−\mathrm{ln}\mid\mathrm{u}\mid+\mathrm{k} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{ln}\mid\mathrm{cos}{x}\mid+\mathrm{k} \\ $$
Commented by joki last updated on 02/Dec/20

$${thank}\:{sir} \\ $$
