Question Number 124353 by ajfour last updated on 02/Dec/20
Commented by ajfour last updated on 02/Dec/20
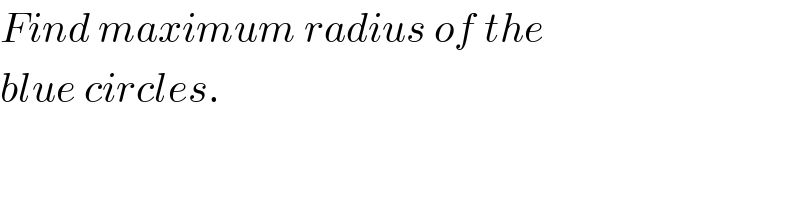
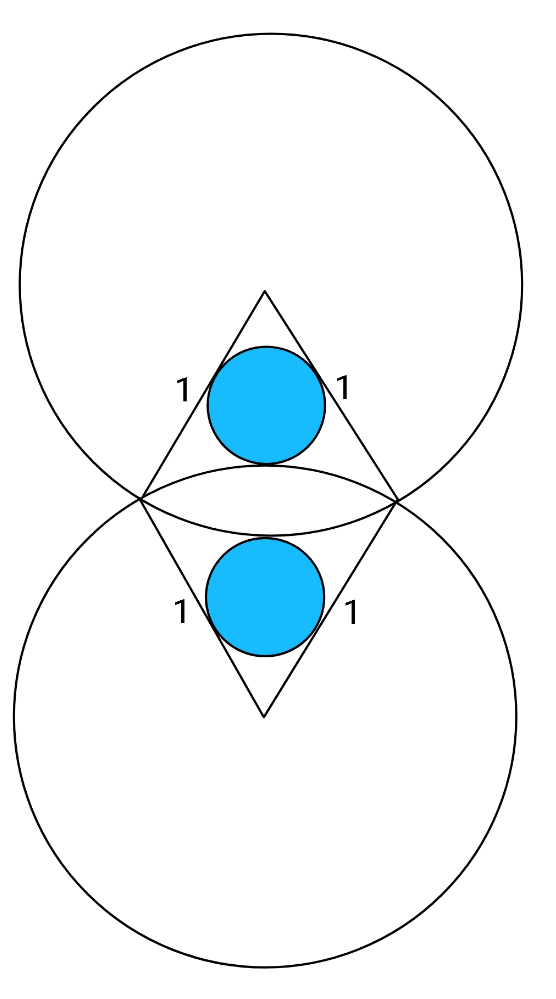
$${Find}\:{maximum}\:{radius}\:{of}\:{the} \\ $$$${blue}\:{circles}. \\ $$
Answered by ajfour last updated on 02/Dec/20
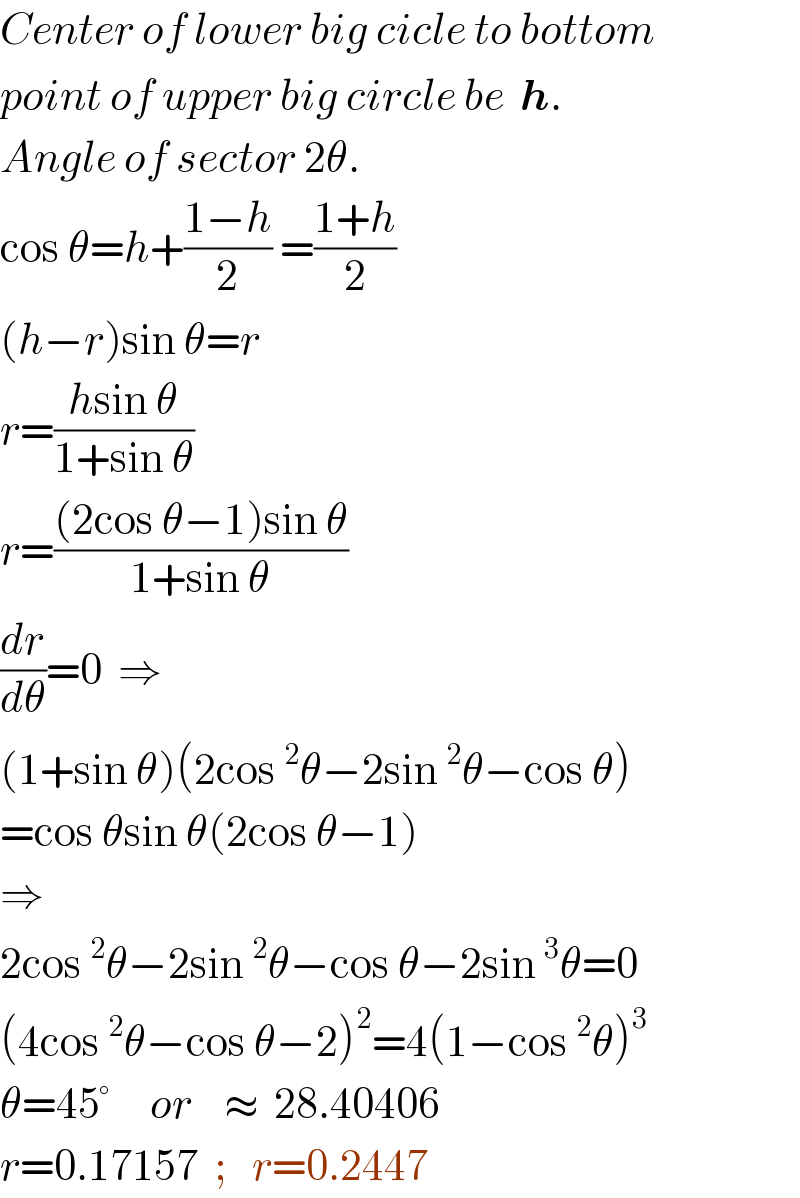
$${Center}\:{of}\:{lower}\:{big}\:{cicle}\:{to}\:{bottom} \\ $$$${point}\:{of}\:{upper}\:{big}\:{circle}\:{be}\:\:\boldsymbol{{h}}. \\ $$$${Angle}\:{of}\:{sector}\:\mathrm{2}\theta. \\ $$$$\mathrm{cos}\:\theta={h}+\frac{\mathrm{1}−{h}}{\mathrm{2}}\:=\frac{\mathrm{1}+{h}}{\mathrm{2}} \\ $$$$\left({h}−{r}\right)\mathrm{sin}\:\theta={r} \\ $$$${r}=\frac{{h}\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta} \\ $$$${r}=\frac{\left(\mathrm{2cos}\:\theta−\mathrm{1}\right)\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta} \\ $$$$\frac{{dr}}{{d}\theta}=\mathrm{0}\:\:\Rightarrow\:\:\: \\ $$$$\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\left(\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{cos}\:\theta\right) \\ $$$$=\mathrm{cos}\:\theta\mathrm{sin}\:\theta\left(\mathrm{2cos}\:\theta−\mathrm{1}\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{cos}\:\theta−\mathrm{2sin}\:^{\mathrm{3}} \theta=\mathrm{0} \\ $$$$\left(\mathrm{4cos}\:^{\mathrm{2}} \theta−\mathrm{cos}\:\theta−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right)^{\mathrm{3}} \\ $$$$\theta=\mathrm{45}°\:\:\:\:\:{or}\:\:\:\:\approx\:\:\mathrm{28}.\mathrm{40406} \\ $$$${r}=\mathrm{0}.\mathrm{17157}\:\:;\:\:\:{r}=\mathrm{0}.\mathrm{2447} \\ $$
Commented by MJS_new last updated on 02/Dec/20

$$\mathrm{I}\:\mathrm{tried}\:\mathrm{with}\:\mathrm{the}\:\mathrm{coordinate}\:\mathrm{method}\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{centers}\:\mathrm{of}\:\mathrm{the}\:\mathrm{big}\:\mathrm{circles}\:\pm{p}\:\mathrm{from}\:\mathrm{the}\:\mathrm{origin} \\ $$$$\mathrm{with}\:\frac{\mathrm{1}}{\mathrm{2}}<{p}<\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{blue}\:\mathrm{circle}\:\mathrm{is} \\ $$$${r}=\frac{\mathrm{2}{p}−\mathrm{1}}{{p}^{\mathrm{2}} }\sqrt{\left({p}^{\mathrm{2}} −\mathrm{1}\right)\left({p}^{\mathrm{2}} −\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\right.} \\ $$$$\mathrm{its}\:\mathrm{maximum}\:\mathrm{is}\:\mathrm{at}\:{p}\:\mathrm{being}\:\mathrm{the}\:\mathrm{real}\:\mathrm{solution} \\ $$$$\mathrm{of}\:{p}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}}{p}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\:{p}=\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}}+\sqrt[{\mathrm{3}}]{−\mathrm{1}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}}\approx.\mathrm{879614880} \\ $$$$\Rightarrow\:{r}\approx.\mathrm{244737182} \\ $$
Commented by mnjuly1970 last updated on 03/Dec/20
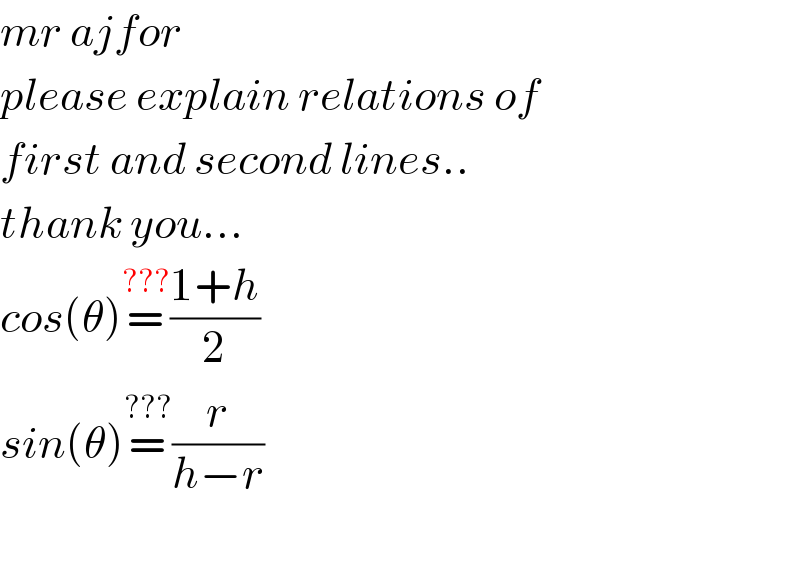
$${mr}\:{ajfor} \\ $$$${please}\:{explain}\:{relations}\:{of} \\ $$$${first}\:{and}\:{second}\:{lines}..\: \\ $$$${thank}\:{you}… \\ $$$${cos}\left(\theta\right)\overset{???} {=}\frac{\mathrm{1}+{h}}{\mathrm{2}} \\ $$$${sin}\left(\theta\right)\overset{???} {=}\frac{{r}}{{h}−{r}} \\ $$$$\: \\ $$
Commented by ajfour last updated on 05/Dec/20

$${great}\:{way},\:{thanks}\:{MjS}\:{Sir}. \\ $$
