Menu Close

Question-124406

Tinku Tara 0 Comments
Pin




Question Number 124406 by joki last updated on 03/Dec/20
Answered by Bird last updated on 03/Dec/20
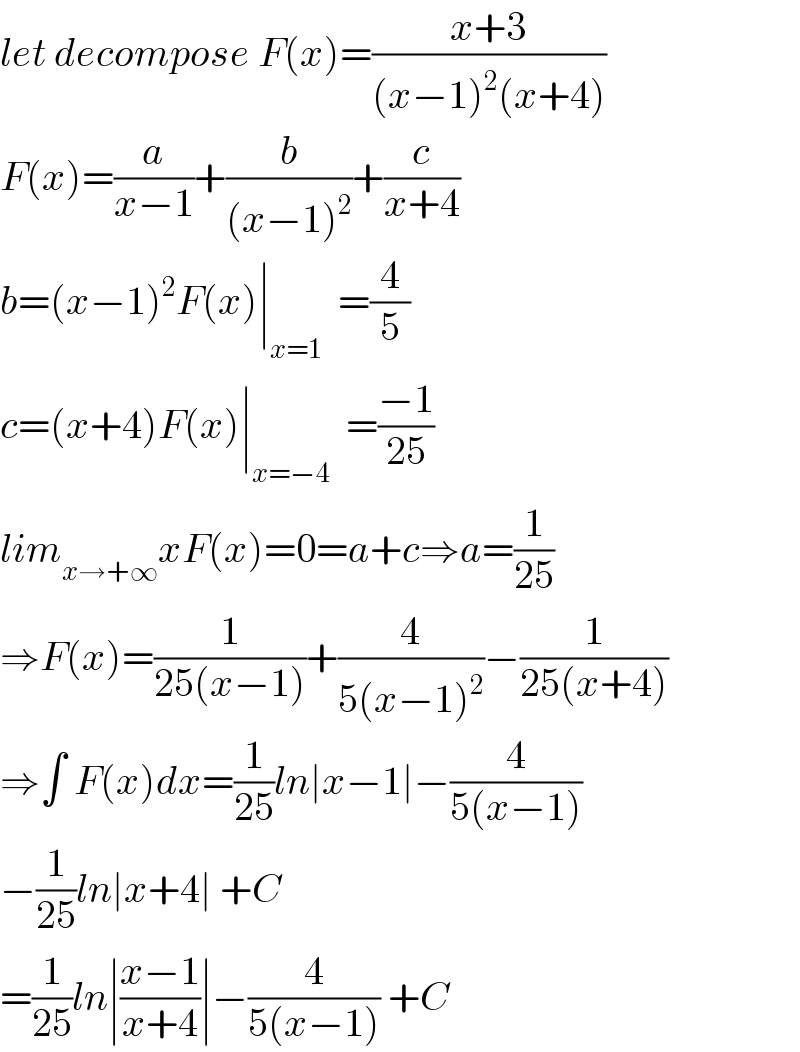
let decompose F(x)=((x+3)/((x−1)^2 (x+4))) F(x)=(a/(x−1))+(b/((x−1)^2 ))+(c/(x+4)) b=(x−1)^2 F(x)∣_(x=1) =(4/5) c=(x+4)F(x)∣_(x=−4) =((−1)/(25)) lim_(x→+∞) xF(x)=0=a+c⇒a=(1/(25)) ⇒F(x)=(1/(25(x−1)))+(4/(5(x−1)^2 ))−(1/(25(x+4))) ⇒∫ F(x)dx=(1/(25))ln∣x−1∣−(4/(5(x−1))) −(1/(25))ln∣x+4∣ +C =(1/(25))ln∣((x−1)/(x+4))∣−(4/(5(x−1))) +C
$${let}\:{decompose}\:{F}\left({x}\right)=\frac{{x}+\mathrm{3}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{4}\right)} \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}−\mathrm{1}}+\frac{{b}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{{c}}{{x}+\mathrm{4}} \\ $$$${b}=\left({x}−\mathrm{1}\right)^{\mathrm{2}} {F}\left({x}\right)\mid_{{x}=\mathrm{1}} \:\:=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${c}=\left({x}+\mathrm{4}\right){F}\left({x}\right)\mid_{{x}=−\mathrm{4}} \:\:=\frac{−\mathrm{1}}{\mathrm{25}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{0}={a}+{c}\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{25}} \\ $$$$\Rightarrow{F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{25}\left({x}−\mathrm{1}\right)}+\frac{\mathrm{4}}{\mathrm{5}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{25}\left({x}+\mathrm{4}\right)} \\ $$$$\Rightarrow\int\:{F}\left({x}\right){dx}=\frac{\mathrm{1}}{\mathrm{25}}{ln}\mid{x}−\mathrm{1}\mid−\frac{\mathrm{4}}{\mathrm{5}\left({x}−\mathrm{1}\right)} \\ $$$$−\frac{\mathrm{1}}{\mathrm{25}}{ln}\mid{x}+\mathrm{4}\mid\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{25}}{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{4}}\mid−\frac{\mathrm{4}}{\mathrm{5}\left({x}−\mathrm{1}\right)}\:+{C} \\ $$
Answered by MJS_new last updated on 03/Dec/20
∫((x+3)/((x−1)^2 (x+4)))dx= =(4/5)∫(dx/((x−1)^2 ))+(1/(25))∫(dx/(x−1))−(1/(25))∫(dx/(x+4))= =−(4/(5(x−1)))+(1/(25))ln ∣((x−1)/(x+4))∣ +C
$$\int\frac{{x}+\mathrm{3}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{4}\right)}{dx}= \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}\int\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{25}}\int\frac{{dx}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{25}}\int\frac{{dx}}{{x}+\mathrm{4}}= \\ $$$$=−\frac{\mathrm{4}}{\mathrm{5}\left({x}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{25}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{4}}\mid\:+{C} \\ $$
Commented by joki last updated on 03/Dec/20
i dont understand sir ,can you explain with detailed sir. thank you
$${i}\:{dont}\:{understand}\:{sir}\:,{can}\:{you}\:{explain}\:{with} \\ $$$${detailed}\:{sir}.\:{thank}\:{you} \\ $$
Commented by MJS_new last updated on 03/Dec/20
just decompose the fraction
$$\mathrm{just}\:\mathrm{decompose}\:\mathrm{the}\:\mathrm{fraction} \\ $$
Commented by Ar Brandon last updated on 03/Dec/20
��
Commented by Ar Brandon last updated on 03/Dec/20
f(x)=((x+3)/((x−1)^2 (x+4)))=(a/(x−1))+(b/((x−1)^2 ))+(c/(x+4)) =((a(x−1)(x+4)+b(x+4)+c(x−1)^2 )/((x−1)^2 (x+4))) x=1 ⇒ 4=5b, b=(4/5) x=−4 ⇒ −1=25c, c=−(1/(25)) for coef of x^2 we have a+c=0, a=(1/(25)) f(x)=(1/(25(x−1)))+(4/(5(x−1)^2 ))−(1/(25(x+4)))
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}+\mathrm{3}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{4}\right)}=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{1}}+\frac{\mathrm{b}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{c}}{\mathrm{x}+\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{a}\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{4}\right)+\mathrm{b}\left(\mathrm{x}+\mathrm{4}\right)+\mathrm{c}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{4}\right)} \\ $$$$\mathrm{x}=\mathrm{1}\:\Rightarrow\:\mathrm{4}=\mathrm{5b},\:\mathrm{b}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{x}=−\mathrm{4}\:\Rightarrow\:−\mathrm{1}=\mathrm{25c},\:\mathrm{c}=−\frac{\mathrm{1}}{\mathrm{25}} \\ $$$$\mathrm{for}\:\mathrm{coef}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{we}\:\mathrm{have}\:\mathrm{a}+\mathrm{c}=\mathrm{0},\:\mathrm{a}=\frac{\mathrm{1}}{\mathrm{25}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{25}\left(\mathrm{x}−\mathrm{1}\right)}+\frac{\mathrm{4}}{\mathrm{5}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{25}\left(\mathrm{x}+\mathrm{4}\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *