Question Number 124591 by mohammad17 last updated on 04/Dec/20
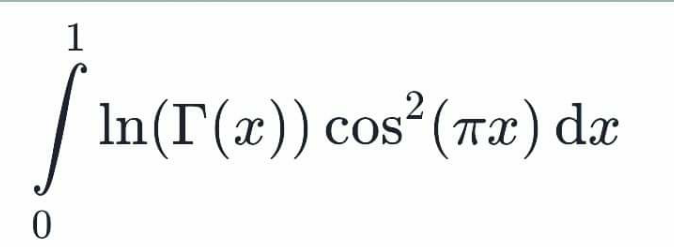
Commented by mohammad17 last updated on 05/Dec/20
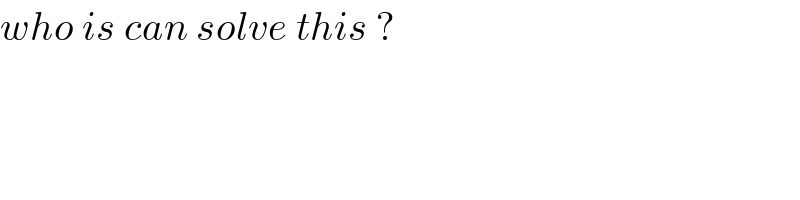
$${who}\:{is}\:{can}\:{solve}\:{this}\:? \\ $$
Answered by mindispower last updated on 05/Dec/20
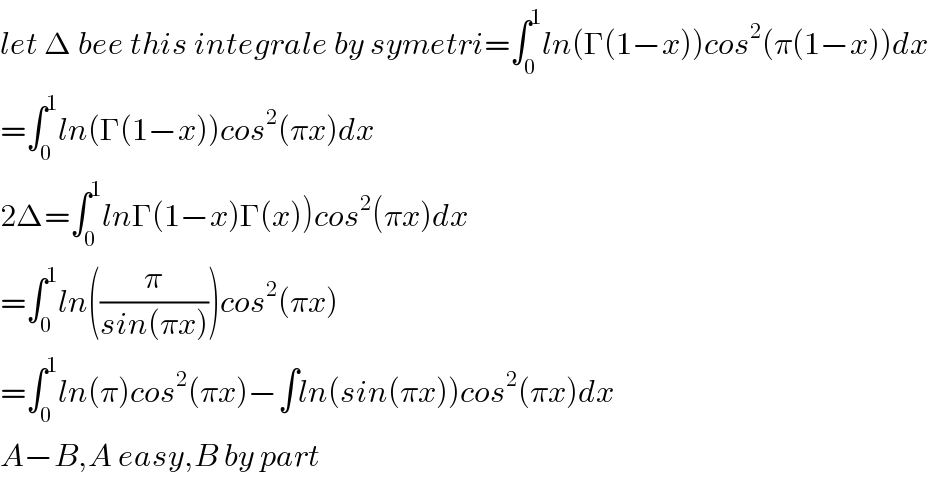
$${let}\:\Delta\:{bee}\:{this}\:{integrale}\:{by}\:{symetri}=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\Gamma\left(\mathrm{1}−{x}\right)\right){cos}^{\mathrm{2}} \left(\pi\left(\mathrm{1}−{x}\right)\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\Gamma\left(\mathrm{1}−{x}\right)\right){cos}^{\mathrm{2}} \left(\pi{x}\right){dx} \\ $$$$\left.\mathrm{2}\Delta=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\Gamma\left(\mathrm{1}−{x}\right)\Gamma\left({x}\right)\right){cos}^{\mathrm{2}} \left(\pi{x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\frac{\pi}{{sin}\left(\pi{x}\right)}\right){cos}^{\mathrm{2}} \left(\pi{x}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\pi\right){cos}^{\mathrm{2}} \left(\pi{x}\right)−\int{ln}\left({sin}\left(\pi{x}\right)\right){cos}^{\mathrm{2}} \left(\pi{x}\right){dx} \\ $$$${A}−{B},{A}\:{easy},{B}\:{by}\:{part} \\ $$
Commented by mohammad17 last updated on 05/Dec/20
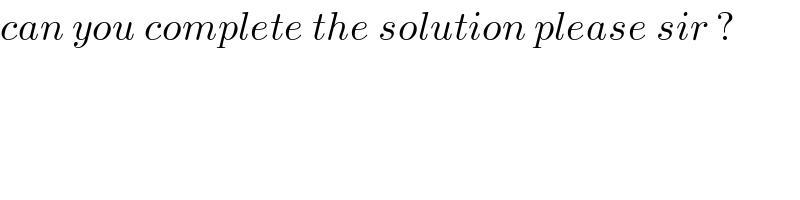
$${can}\:{you}\:{complete}\:{the}\:{solution}\:{please}\:{sir}\:? \\ $$
