Question Number 124698 by Algoritm last updated on 05/Dec/20
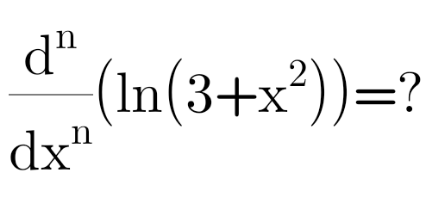
Answered by Olaf last updated on 05/Dec/20
![Let f(x) = ln(3+x^2 ) f(x) = ln∣x−(√3)i∣+ln∣x+(√3)i∣ f′(x) = (1/(x−(√3)i))+(1/(x+(√3)i)) f′′(x) = −(1/((x−(√3)i)^2 ))−(1/((x+(√3)i)^2 )) f^((3)) (x) = ((1.2)/((x−(√3)i)^3 ))+((1.2)/((x+(√3)i)^3 )) f^((4)) (x) = (−1)^3 [((1.2.3)/((x−(√3)i)^4 ))+((1.2.3)/((x+(√3)i)^4 ))] ... f^((n)) (x) = (−1)^(n−1) (n−1)![(1/((x−(√3)i)^n ))+(1/((x+(√3)i)^n ))] x±(√3)i = (√(x^2 +3)).e^(±iarctan((√3)/x)) f^((n)) (x) = (((−1)^(n−1) (n−1)!)/( (√(x^2 +3))))[(1/((e^(−iarctan((√3)/x)) )^n ))+(1/((e^(iarctan((√3)/( x))) )^n ))] f^((n)) (x) = (((−1)^(n−1) (n−1)!)/( (√(x^2 +3))))[(1/e^(−inarctan((√3)/x)) )+(1/e^(inarctan((√3)/( x))) )] f^((n)) (x) = (((−1)^(n−1) (n−1)!)/( (√(x^2 +3))))[e^(inarctan((√3)/x)) +e^(−inarctan((√3)/x)) ] f^((n)) (x) = (((−1)^(n−1) (n−1)!)/( (√(x^2 +3))))[2cos(narctan((√3)/x))] or we can write : f^((n)) (x) = ((2(−1)^(n−1) (n−1)!)/( (√(x^2 +3))))cos[n((π/2)−arctan(x/( (√3))))]](https://www.tinkutara.com/question/Q124715.png)
$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\mathrm{ln}\left(\mathrm{3}+{x}^{\mathrm{2}} \right) \\ $$$${f}\left({x}\right)\:=\:\mathrm{ln}\mid{x}−\sqrt{\mathrm{3}}{i}\mid+\mathrm{ln}\mid{x}+\sqrt{\mathrm{3}}{i}\mid \\ $$$${f}'\left({x}\right)\:=\:\frac{\mathrm{1}}{{x}−\sqrt{\mathrm{3}}{i}}+\frac{\mathrm{1}}{{x}+\sqrt{\mathrm{3}}{i}} \\ $$$${f}''\left({x}\right)\:=\:−\frac{\mathrm{1}}{\left({x}−\sqrt{\mathrm{3}}{i}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({x}+\sqrt{\mathrm{3}}{i}\right)^{\mathrm{2}} } \\ $$$${f}^{\left(\mathrm{3}\right)} \left({x}\right)\:=\:\frac{\mathrm{1}.\mathrm{2}}{\left({x}−\sqrt{\mathrm{3}}{i}\right)^{\mathrm{3}} }+\frac{\mathrm{1}.\mathrm{2}}{\left({x}+\sqrt{\mathrm{3}}{i}\right)^{\mathrm{3}} } \\ $$$${f}^{\left(\mathrm{4}\right)} \left({x}\right)\:=\:\left(−\mathrm{1}\right)^{\mathrm{3}} \left[\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}}{\left({x}−\sqrt{\mathrm{3}}{i}\right)^{\mathrm{4}} }+\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}}{\left({x}+\sqrt{\mathrm{3}}{i}\right)^{\mathrm{4}} }\right] \\ $$$$… \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left[\frac{\mathrm{1}}{\left({x}−\sqrt{\mathrm{3}}{i}\right)^{{n}} }+\frac{\mathrm{1}}{\left({x}+\sqrt{\mathrm{3}}{i}\right)^{{n}} }\right] \\ $$$${x}\pm\sqrt{\mathrm{3}}{i}\:=\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}.{e}^{\pm{i}\mathrm{arctan}\frac{\sqrt{\mathrm{3}}}{{x}}} \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}\left[\frac{\mathrm{1}}{\left({e}^{−{i}\mathrm{arctan}\frac{\sqrt{\mathrm{3}}}{{x}}} \right)^{{n}} }+\frac{\mathrm{1}}{\left({e}^{{i}\mathrm{arctan}\frac{\sqrt{\mathrm{3}}}{\:{x}}} \right)^{{n}} }\right] \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}\left[\frac{\mathrm{1}}{{e}^{−{in}\mathrm{arctan}\frac{\sqrt{\mathrm{3}}}{{x}}} }+\frac{\mathrm{1}}{{e}^{{in}\mathrm{arctan}\frac{\sqrt{\mathrm{3}}}{\:{x}}} }\right] \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}\left[{e}^{{in}\mathrm{arctan}\frac{\sqrt{\mathrm{3}}}{{x}}} +{e}^{−{in}\mathrm{arctan}\frac{\sqrt{\mathrm{3}}}{{x}}} \right] \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}\left[\mathrm{2cos}\left({n}\mathrm{arctan}\frac{\sqrt{\mathrm{3}}}{{x}}\right)\right] \\ $$$$\mathrm{or}\:\mathrm{we}\:\mathrm{can}\:\mathrm{write}\:: \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\:\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}\mathrm{cos}\left[{n}\left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\frac{{x}}{\:\sqrt{\mathrm{3}}}\right)\right] \\ $$
Answered by TANMAY PANACEA last updated on 05/Dec/20
![y=ln(3+x^2 ) y_1 =((2x)/(3+x^2 ))=((2x)/((x+i(√3) )(x−i(√3) )))=(1/((x+i(√3) )))+(1/((x−i(√(3)))))=(1/(x+a))+(1/(x−a)) y_1 =(x+a)^(−1) +(x−a)^(−1) y_2 =(−1)(x+a)^(−2) +(−1)(x−a)^(−2) y_3 =(−1)(−2)(x+a)^(−3) +(−1)(−2)(x−a)^(−3) ... ... y_n =(−1)(−2)...{−(n−1)}[(x+a)^(−n) +(x−a)^(−n) ] y_n =(−1)^(n−1) (n−1)![(x+i(√3) )^(−n) +(x−i(√3) )^(−n) ]](https://www.tinkutara.com/question/Q124711.png)
$${y}={ln}\left(\mathrm{3}+{x}^{\mathrm{2}} \right) \\ $$$${y}_{\mathrm{1}} =\frac{\mathrm{2}{x}}{\mathrm{3}+{x}^{\mathrm{2}} }=\frac{\mathrm{2}{x}}{\left({x}+{i}\sqrt{\mathrm{3}}\:\right)\left({x}−{i}\sqrt{\mathrm{3}}\:\right)}=\frac{\mathrm{1}}{\left({x}+{i}\sqrt{\mathrm{3}}\:\right)}+\frac{\mathrm{1}}{\left({x}−{i}\sqrt{\left.\mathrm{3}\right)}\right.}=\frac{\mathrm{1}}{{x}+{a}}+\frac{\mathrm{1}}{{x}−{a}} \\ $$$${y}_{\mathrm{1}} =\left({x}+{a}\right)^{−\mathrm{1}} +\left({x}−{a}\right)^{−\mathrm{1}} \\ $$$${y}_{\mathrm{2}} =\left(−\mathrm{1}\right)\left({x}+{a}\right)^{−\mathrm{2}} +\left(−\mathrm{1}\right)\left({x}−{a}\right)^{−\mathrm{2}} \\ $$$${y}_{\mathrm{3}} =\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)\left({x}+{a}\right)^{−\mathrm{3}} +\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)\left({x}−{a}\right)^{−\mathrm{3}} \\ $$$$… \\ $$$$… \\ $$$${y}_{{n}} =\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)…\left\{−\left({n}−\mathrm{1}\right)\right\}\left[\left({x}+{a}\right)^{−{n}} +\left({x}−{a}\right)^{−{n}} \right] \\ $$$${y}_{{n}} =\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left[\left({x}+{i}\sqrt{\mathrm{3}}\:\right)^{−{n}} +\left({x}−{i}\sqrt{\mathrm{3}}\:\right)^{−{n}} \right] \\ $$
Answered by Bird last updated on 05/Dec/20
![f(x)=ln(x^2 +3) ⇒ f^((1)) (x)=((2x)/(x^2 +3))=((2x)/((x−i(√3))(x+i(√3)))) =(1/(x−i(√3)))+(1/(x+i(√3))) ⇒ f^((n)) (x)=((1/(x−i(√3))))^((n−1)) +((1/(x+i(√3))))^((n−1)) =(((−1)^(n−1) (n−1)!)/((x−i(√3))^n ))+(((−1)^(n−1) (n−1)!)/((x+i(√3))^n )) =(−1)^(n−1) (n−1)!{(1/((x−i(√3))^n ))+(1/((x+i(√3))^n ))} =(−1)^(n−1) (n−1)!×(((x+i(√3))^n +(x−i(√3))^n )/((x^2 +3)^n )) f^((n)) (x)=(−1)^(n−1) (n−1)!((2Re((x+i(√3))^n ))/((x^2 +3)^n )) with n≥1 we have (x+i(√3))^n =Σ_(k=0) ^n C_n ^k (i(√3))^k x^(n−k) =Σ_(p=0) ^([(n/2)] ) C_n ^(2p) (−1)^p 3^p x^(n−2p) +is(x) ⇒Re((x+i(√3))^n ) =Σ_(p=0) ^([(n/2)(√)) (−1)^p 3^p C_n ^(2p ) x^(n−2p)](https://www.tinkutara.com/question/Q124770.png)
$${f}\left({x}\right)={ln}\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)\:\Rightarrow \\ $$$${f}^{\left(\mathrm{1}\right)} \left({x}\right)=\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\mathrm{3}}=\frac{\mathrm{2}{x}}{\left({x}−{i}\sqrt{\mathrm{3}}\right)\left({x}+{i}\sqrt{\mathrm{3}}\right)} \\ $$$$=\frac{\mathrm{1}}{{x}−{i}\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{{x}+{i}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\left(\frac{\mathrm{1}}{{x}−{i}\sqrt{\mathrm{3}}}\right)^{\left({n}−\mathrm{1}\right)} +\left(\frac{\mathrm{1}}{{x}+{i}\sqrt{\mathrm{3}}}\right)^{\left({n}−\mathrm{1}\right)} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−{i}\sqrt{\mathrm{3}}\right)^{{n}} }+\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}} } \\ $$$$=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left\{\frac{\mathrm{1}}{\left({x}−{i}\sqrt{\mathrm{3}}\right)^{{n}} }+\frac{\mathrm{1}}{\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}} }\right\} \\ $$$$=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!×\frac{\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}} +\left({x}−{i}\sqrt{\mathrm{3}}\right)^{{n}} }{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{{n}} } \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\frac{\mathrm{2}{Re}\left(\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}} \right)}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{{n}} } \\ $$$${with}\:{n}\geqslant\mathrm{1} \\ $$$${we}\:{have}\:\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}} \:=\sum_{{k}=\mathrm{0}} ^{{n}} {C}_{{n}} ^{{k}} \left({i}\sqrt{\mathrm{3}}\right)^{{k}} {x}^{{n}−{k}} \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]\:} {C}_{{n}} ^{\mathrm{2}{p}} \left(−\mathrm{1}\right)^{{p}} \:\mathrm{3}^{{p}} \:{x}^{{n}−\mathrm{2}{p}} \:+{is}\left({x}\right) \\ $$$$\Rightarrow{Re}\left(\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}} \right) \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\sqrt{}\right.} \:\left(−\mathrm{1}\right)^{{p}} \:\mathrm{3}^{{p}} \:{C}_{{n}} ^{\mathrm{2}{p}\:} {x}^{{n}−\mathrm{2}{p}} \\ $$
