Question-124740

Question Number 124740 by ajfour last updated on 05/Dec/20

Commented by ajfour last updated on 05/Dec/20

Find eq. of circle passing through intersection points of curves y=x^2 −1 and y=(c/x) ; (c < (2/(3(√3))))

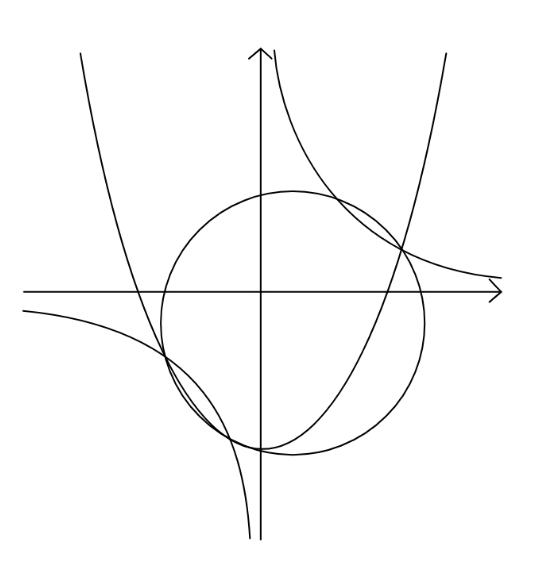
$${Find}\:{eq}.\:{of}\:{circle}\:{passing}\:{through} \\ $$$${intersection}\:{points}\:{of}\:\:{curves} \\ $$$${y}={x}^{\mathrm{2}} −\mathrm{1}\:\:{and}\:\:{y}=\frac{{c}}{{x}}\:;\:\:\:\left({c}\:<\:\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\right) \\ $$

Answered by ajfour last updated on 05/Dec/20

y=x^2 −1 y=(c/x) let roots of x^2 −1=(c/x) be p, q, r p+q+r=0 pq+qr+rp=−1 pqr=c (y−k)^2 +(x−h)^2 =R^( 2) (x^2 −1−k)^2 +(x−h)^2 =R^( 2) p(q^2 +r^2 −2−k)+p+2h=0 ⇒ p(p^2 −((2c)/p)−2−k)+p+2h=0 ⇒ 2h−(k+2)p+2p−c=0 ....(I) ⇒ Σ gives ⇒ h=(c/2) And considering (I) again with h=c ⇒ k=0 ⇒ R^( 2) = (x^2 −1)^2 +(x−(c/2))^2 ⇒ R^( 2) = 1+(c^2 /4) Hence eq. of circle is (x−(c/2))^2 +y^2 =1+(c^2 /4) example: For c=(1/3) , the curves are y=x^2 −1 , y=(1/(3x)) , and the circle (x−(1/6))^2 +y^2 =((37)/(36)) ★

$${y}={x}^{\mathrm{2}} −\mathrm{1} \\ $$$${y}=\frac{{c}}{{x}} \\ $$$${let}\:{roots}\:{of}\:\:{x}^{\mathrm{2}} −\mathrm{1}=\frac{{c}}{{x}}\:\:\:{be}\:\:{p},\:{q},\:{r} \\ $$$${p}+{q}+{r}=\mathrm{0} \\ $$$${pq}+{qr}+{rp}=−\mathrm{1} \\ $$$${pqr}={c} \\ $$$$\left({y}−{k}\right)^{\mathrm{2}} +\left({x}−{h}\right)^{\mathrm{2}} ={R}^{\:\mathrm{2}} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{1}−{k}\right)^{\mathrm{2}} +\left({x}−{h}\right)^{\mathrm{2}} ={R}^{\:\mathrm{2}} \\ $$$${p}\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}−{k}\right)+{p}+\mathrm{2}{h}=\mathrm{0} \\ $$$$\Rightarrow\:\:{p}\left({p}^{\mathrm{2}} −\frac{\mathrm{2}{c}}{{p}}−\mathrm{2}−{k}\right)+{p}+\mathrm{2}{h}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2}{h}−\left({k}+\mathrm{2}\right){p}+\mathrm{2}{p}−{c}=\mathrm{0}\:\:\:….\left({I}\right) \\ $$$$\Rightarrow\:\Sigma\:\:{gives} \\ $$$$\Rightarrow\:\:\:\:{h}=\frac{{c}}{\mathrm{2}} \\ $$$${And}\:{considering}\:\left({I}\right)\:{again} \\ $$$${with}\:\:{h}={c}\:\:\Rightarrow\:\:\:{k}=\mathrm{0} \\ $$$$\Rightarrow\:\:{R}^{\:\mathrm{2}} \:=\:\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\left({x}−\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{R}^{\:\mathrm{2}} =\:\mathrm{1}+\frac{{c}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${Hence}\:{eq}.\:{of}\:{circle}\:{is} \\ $$$$\:\:\left({x}−\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}+\frac{{c}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${example}: \\ $$$${For}\:\:\:{c}=\frac{\mathrm{1}}{\mathrm{3}}\:\:,\:{the}\:{curves}\:{are} \\ $$$${y}={x}^{\mathrm{2}} −\mathrm{1}\:\:,\:\:{y}=\frac{\mathrm{1}}{\mathrm{3}{x}}\:,\:\:{and}\:{the}\:{circle} \\ $$$$\left({x}−\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\frac{\mathrm{37}}{\mathrm{36}}\:\:\:\bigstar \\ $$

Commented by ajfour last updated on 05/Dec/20