Question Number 124743 by ajfour last updated on 05/Dec/20
Commented by ajfour last updated on 05/Dec/20
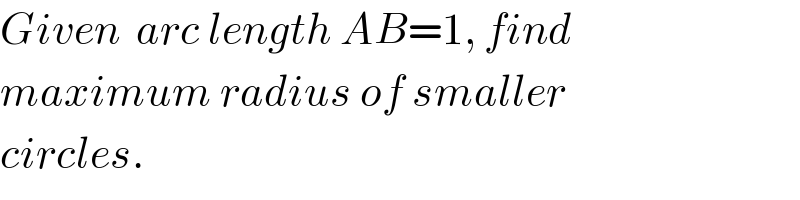
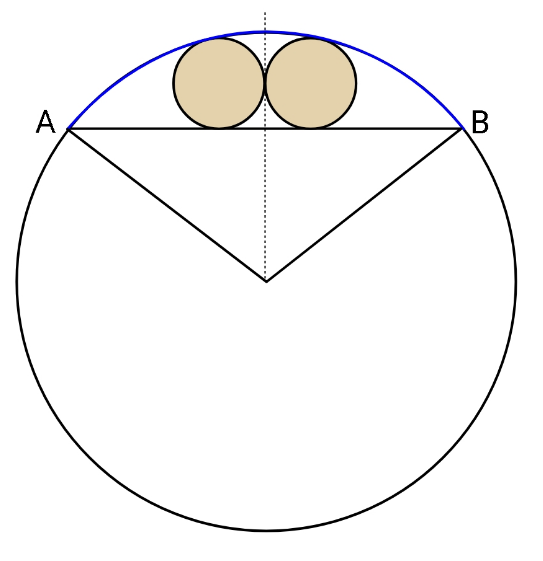
$${Given}\:\:{arc}\:{length}\:{AB}=\mathrm{1},\:{find} \\ $$$${maximum}\:{radius}\:{of}\:{smaller} \\ $$$${circles}. \\ $$
Answered by mr W last updated on 05/Dec/20

Commented by mr W last updated on 05/Dec/20
![2θR=1 θ=(1/(2R)) (R−r)^2 =r^2 +(r+R cos θ)^2 r^2 +2R(1+cos θ)r−R^2 (1−cos^2 θ)=0 r=R[(√(2(1+cos θ)))−(1+cos θ)] r=(1/(2θ))[(√(2(1+cos θ)))−(1+cos θ)] at θ=(π/2): r_(max) =(((√2)−1)/π)](https://www.tinkutara.com/question/Q124759.png)
$$\mathrm{2}\theta{R}=\mathrm{1} \\ $$$$\theta=\frac{\mathrm{1}}{\mathrm{2}{R}} \\ $$$$\left({R}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} +\left({r}+{R}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} +\mathrm{2}{R}\left(\mathrm{1}+\mathrm{cos}\:\theta\right){r}−{R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)=\mathrm{0} \\ $$$${r}={R}\left[\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}−\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\right] \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{2}\theta}\left[\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}−\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\right] \\ $$$${at}\:\theta=\frac{\pi}{\mathrm{2}}: \\ $$$${r}_{{max}} =\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\pi} \\ $$
Commented by ajfour last updated on 05/Dec/20
sir how did you confirm, i tried grapher, it draws weird graph...
Commented by mr W last updated on 06/Dec/20

$${we}\:{got}\:{the}\:{same}\:{function}\:{for}\:{r} \\ $$$${in}\:{terms}\:{of}\:\theta: \\ $$$${r}=\frac{\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}−\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}{\mathrm{2}\theta} \\ $$$${for}\:\mathrm{0}<\theta\leqslant\pi/\mathrm{2}\:{the}\:{function}\:{is} \\ $$$${increasing},\:{therefore}\:{r}_{{max}} \:{is}\:{at}\:\theta=\frac{\pi}{\mathrm{2}}. \\ $$$${because}\:{segment}\:{is}\:{defined}\:{for} \\ $$$$\mathrm{0}<\theta\leqslant\pi/\mathrm{2}. \\ $$
Commented by mr W last updated on 05/Dec/20
Commented by ajfour last updated on 05/Dec/20

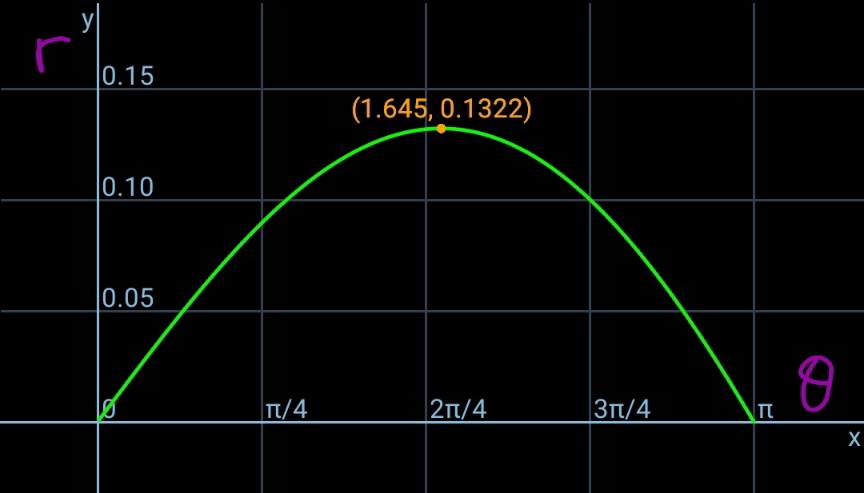
$$\frac{\pi}{\mathrm{2}}\approx\:\mathrm{1}.\mathrm{57079}\: \\ $$
Commented by mr W last updated on 06/Dec/20

$${that}'{s}\:{what}\:{i}\:{meant}.\:{we}\:{can}\:{not}\:{get} \\ $$$${the}\:{mathematical}\:{maximum}\:{at} \\ $$$$\theta=\mathrm{1}.\mathrm{645},\:{because}\:{that}\:{is}\:{behind}\: \\ $$$$\theta=\frac{\pi}{\mathrm{2}},\:{the}\:{possible}\:{segment}. \\ $$$${the}\:{actual}\:{maximum}\:{we}\:{can}\:{reach} \\ $$$${is}\:{at}\:\theta=\frac{\pi}{\mathrm{2}}:\:{r}_{{max}} =\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\pi}\:{which}\:{is} \\ $$$${less}\:{than}\:\mathrm{0}.\mathrm{1322}. \\ $$
Commented by ajfour last updated on 06/Dec/20

$${I}\:{guess},\:{i}\:{follow}\:{now},\:{Sir}! \\ $$$${you}\:{make}\:{it}\:{quite}\:{clear},\:\mathcal{T}{hanks}. \\ $$
