Question Number 124779 by TITA last updated on 05/Dec/20

Commented by TITA last updated on 05/Dec/20

$${please}\:{help} \\ $$
Answered by Lordose last updated on 06/Dec/20
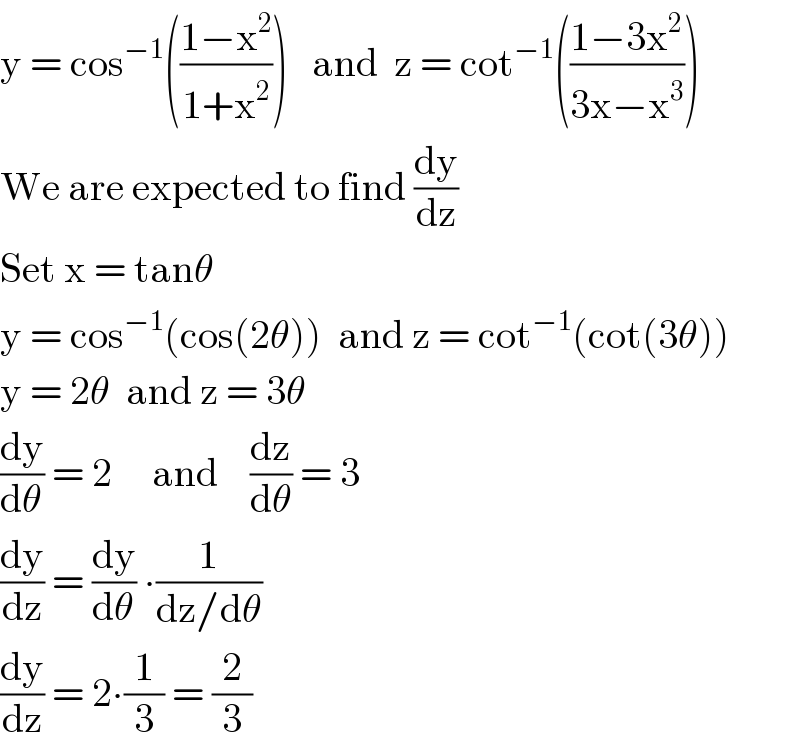
$$\mathrm{y}\:=\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\:\:\:\mathrm{and}\:\:\mathrm{z}\:=\:\mathrm{cot}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\mathrm{3x}^{\mathrm{2}} }{\mathrm{3x}−\mathrm{x}^{\mathrm{3}} }\right) \\ $$$$\mathrm{We}\:\mathrm{are}\:\mathrm{expected}\:\mathrm{to}\:\mathrm{find}\:\frac{\mathrm{dy}}{\mathrm{dz}} \\ $$$$\mathrm{Set}\:\mathrm{x}\:=\:\mathrm{tan}\theta \\ $$$$\mathrm{y}\:=\:\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{cos}\left(\mathrm{2}\theta\right)\right)\:\:\mathrm{and}\:\mathrm{z}\:=\:\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{cot}\left(\mathrm{3}\theta\right)\right) \\ $$$$\mathrm{y}\:=\:\mathrm{2}\theta\:\:\mathrm{and}\:\mathrm{z}\:=\:\mathrm{3}\theta \\ $$$$\frac{\mathrm{dy}}{\mathrm{d}\theta}\:=\:\mathrm{2}\:\:\:\:\:\mathrm{and}\:\:\:\:\frac{\mathrm{dz}}{\mathrm{d}\theta}\:=\:\mathrm{3} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dz}}\:=\:\frac{\mathrm{dy}}{\mathrm{d}\theta}\:\centerdot\frac{\mathrm{1}}{\mathrm{dz}/\mathrm{d}\theta} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dz}}\:=\:\mathrm{2}\centerdot\frac{\mathrm{1}}{\mathrm{3}}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by TITA last updated on 06/Dec/20

$${thanks} \\ $$
