Menu Close

Question-124806

Tinku Tara 0 Comments
Pin




Question Number 124806 by bramlexs22 last updated on 06/Dec/20
Answered by mr W last updated on 06/Dec/20
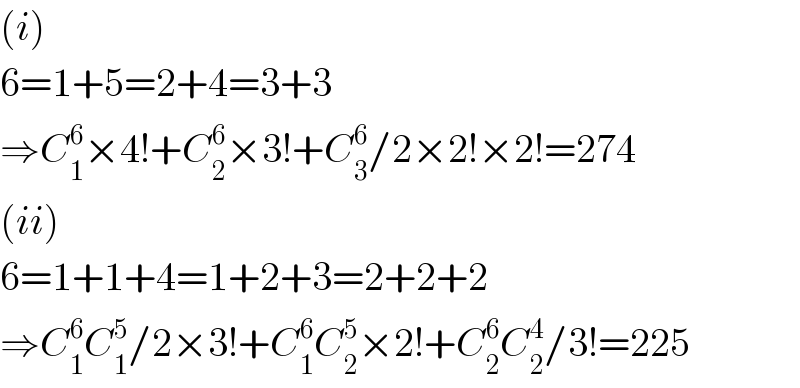
(i) 6=1+5=2+4=3+3 ⇒C_1 ^6 ×4!+C_2 ^6 ×3!+C_3 ^6 /2×2!×2!=274 (ii) 6=1+1+4=1+2+3=2+2+2 ⇒C_1 ^6 C_1 ^5 /2×3!+C_1 ^6 C_2 ^5 ×2!+C_2 ^6 C_2 ^4 /3!=225
$$\left({i}\right) \\ $$$$\mathrm{6}=\mathrm{1}+\mathrm{5}=\mathrm{2}+\mathrm{4}=\mathrm{3}+\mathrm{3} \\ $$$$\Rightarrow{C}_{\mathrm{1}} ^{\mathrm{6}} ×\mathrm{4}!+{C}_{\mathrm{2}} ^{\mathrm{6}} ×\mathrm{3}!+{C}_{\mathrm{3}} ^{\mathrm{6}} /\mathrm{2}×\mathrm{2}!×\mathrm{2}!=\mathrm{274} \\ $$$$\left({ii}\right) \\ $$$$\mathrm{6}=\mathrm{1}+\mathrm{1}+\mathrm{4}=\mathrm{1}+\mathrm{2}+\mathrm{3}=\mathrm{2}+\mathrm{2}+\mathrm{2} \\ $$$$\Rightarrow{C}_{\mathrm{1}} ^{\mathrm{6}} {C}_{\mathrm{1}} ^{\mathrm{5}} /\mathrm{2}×\mathrm{3}!+{C}_{\mathrm{1}} ^{\mathrm{6}} {C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{2}!+{C}_{\mathrm{2}} ^{\mathrm{6}} {C}_{\mathrm{2}} ^{\mathrm{4}} /\mathrm{3}!=\mathrm{225} \\ $$
Commented by john_santu last updated on 06/Dec/20
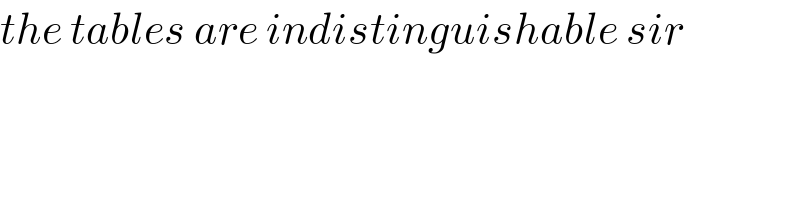
the tables are indistinguishable sir
$${the}\:{tables}\:{are}\:{indistinguishable}\:{sir} \\ $$
Commented by mr W last updated on 06/Dec/20
yes, now i see it. please check again.
$${yes},\:{now}\:{i}\:{see}\:{it}.\:{please}\:{check}\:{again}. \\ $$
Commented by john_santu last updated on 06/Dec/20
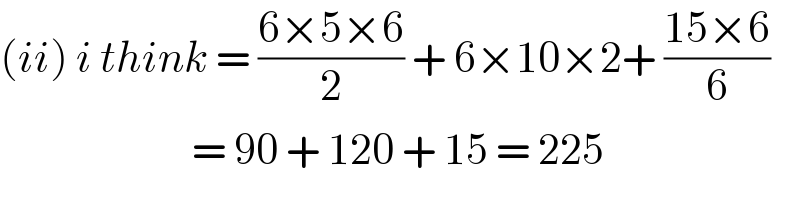
(ii) i think = ((6×5×6)/2) + 6×10×2+ ((15×6)/6) = 90 + 120 + 15 = 225
$$\left({ii}\right)\:{i}\:{think}\:=\:\frac{\mathrm{6}×\mathrm{5}×\mathrm{6}}{\mathrm{2}}\:+\:\mathrm{6}×\mathrm{10}×\mathrm{2}+\:\frac{\mathrm{15}×\mathrm{6}}{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{90}\:+\:\mathrm{120}\:+\:\mathrm{15}\:=\:\mathrm{225} \\ $$
Commented by john_santu last updated on 06/Dec/20
ok sir. thank you
$${ok}\:{sir}.\:{thank}\:{you} \\ $$
Commented by bramlexs22 last updated on 06/Dec/20
thank you both sir
$${thank}\:{you}\:{both}\:{sir} \\ $$
Answered by john_santu last updated on 06/Dec/20
(i) For 2 tables there are 3 cases to consider according to the numbers of people to be seated arround the 2 respective tables, namely (1) 5+1 (2) 4+2 (3) 3+3 case(1) There C _5^6 ×4!×0! = 144 case(2) There C _4^6 ×3! ×1! = 90 case(3) There ((C _3^6 )/(2!)) × 2!×2! = 40 the desired number of arrangements is 144 + 90 + 40 = 274.
$$\left({i}\right)\:{For}\:\mathrm{2}\:{tables}\:{there}\:{are}\:\mathrm{3}\:{cases}\:{to}\:{consider} \\ $$$${according}\:{to}\:{the}\:{numbers}\:{of}\:{people}\:{to}\:{be} \\ $$$${seated}\:{arround}\:{the}\:\mathrm{2}\:{respective}\:{tables},\:{namely} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{5}+\mathrm{1}\:\:\:\:\:\:\:\left(\mathrm{2}\right)\:\mathrm{4}+\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}\right)\:\mathrm{3}+\mathrm{3}\: \\ $$$${case}\left(\mathrm{1}\right)\:{There}\:{C}\:_{\mathrm{5}} ^{\mathrm{6}} \:×\mathrm{4}!×\mathrm{0}!\:=\:\mathrm{144} \\ $$$${case}\left(\mathrm{2}\right)\:{There}\:{C}\:_{\mathrm{4}} ^{\mathrm{6}} \:×\mathrm{3}!\:×\mathrm{1}!\:=\:\mathrm{90} \\ $$$${case}\left(\mathrm{3}\right)\:{There}\:\frac{{C}\:_{\mathrm{3}} ^{\mathrm{6}} }{\mathrm{2}!}\:×\:\mathrm{2}!×\mathrm{2}!\:=\:\mathrm{40} \\ $$$${the}\:{desired}\:{number}\:{of}\:{arrangements}\: \\ $$$$\:{is}\:\mathrm{144}\:+\:\mathrm{90}\:+\:\mathrm{40}\:=\:\mathrm{274}.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *