Question Number 124820 by enter last updated on 06/Dec/20

Answered by mr W last updated on 13/Jun/21
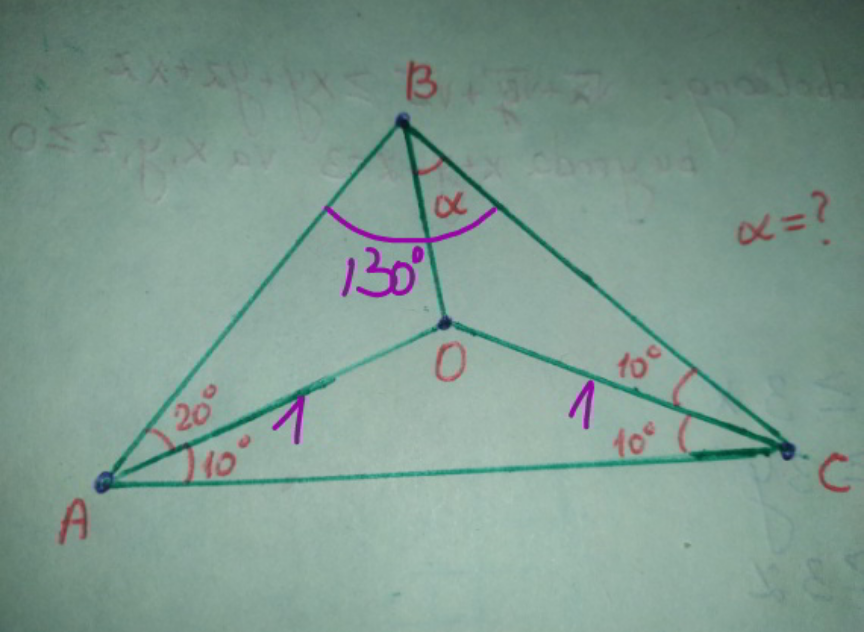
Commented by mr W last updated on 13/Jun/21
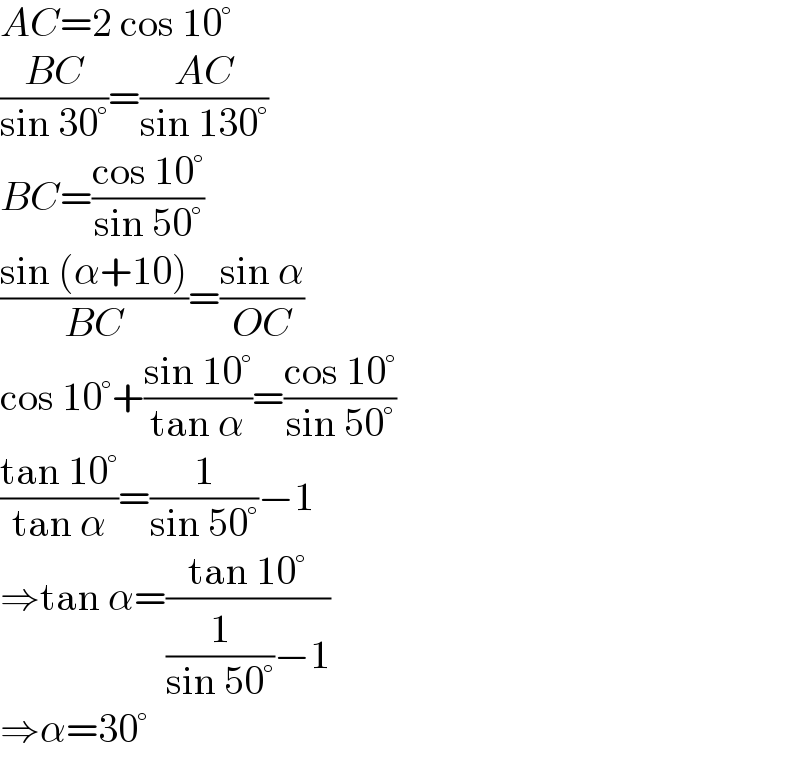
$${AC}=\mathrm{2}\:\mathrm{cos}\:\mathrm{10}° \\ $$$$\frac{{BC}}{\mathrm{sin}\:\mathrm{30}°}=\frac{{AC}}{\mathrm{sin}\:\mathrm{130}°} \\ $$$${BC}=\frac{\mathrm{cos}\:\mathrm{10}°}{\mathrm{sin}\:\mathrm{50}°} \\ $$$$\frac{\mathrm{sin}\:\left(\alpha+\mathrm{10}\right)}{{BC}}=\frac{\mathrm{sin}\:\alpha}{{OC}} \\ $$$$\mathrm{cos}\:\mathrm{10}°+\frac{\mathrm{sin}\:\mathrm{10}°}{\mathrm{tan}\:\alpha}=\frac{\mathrm{cos}\:\mathrm{10}°}{\mathrm{sin}\:\mathrm{50}°} \\ $$$$\frac{\mathrm{tan}\:\mathrm{10}°}{\mathrm{tan}\:\alpha}=\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{50}°}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{tan}\:\mathrm{10}°}{\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{50}°}−\mathrm{1}} \\ $$$$\Rightarrow\alpha=\mathrm{30}° \\ $$
