Menu Close

Question-124957

Tinku Tara 0 Comments
Pin




Question Number 124957 by Study last updated on 07/Dec/20
Commented by Study last updated on 07/Dec/20
please help me??
$${please}\:{help}\:{me}?? \\ $$
Answered by Dwaipayan Shikari last updated on 07/Dec/20
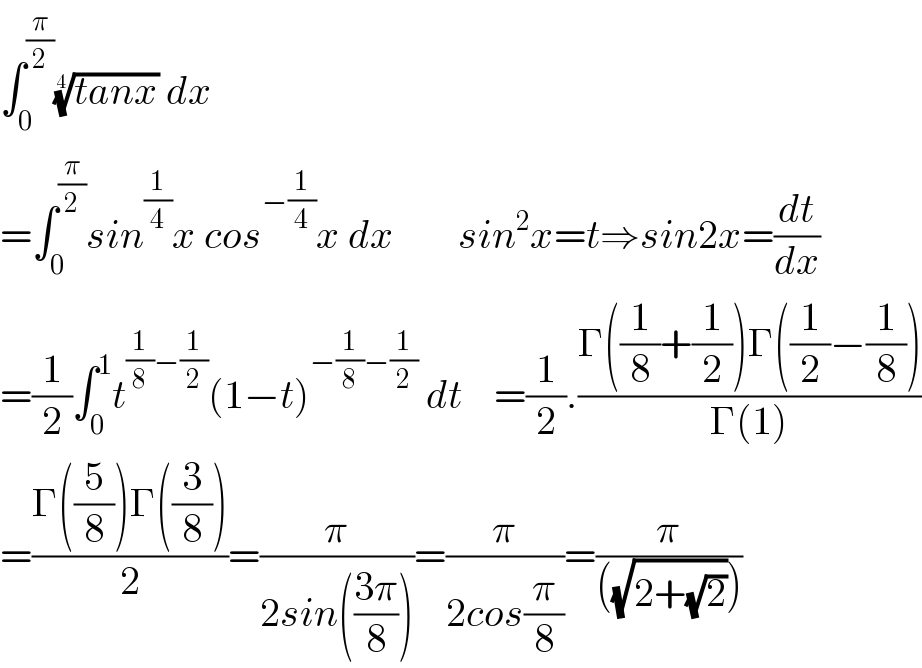
∫_0 ^(π/2) ((tanx))^(1/4) dx =∫_0 ^(π/2) sin^(1/4) x cos^(−(1/4)) x dx sin^2 x=t⇒sin2x=(dt/dx) =(1/2)∫_0 ^1 t^((1/8)−(1/2)) (1−t)^(−(1/8)−(1/2)) dt =(1/2).((Γ((1/8)+(1/2))Γ((1/2)−(1/8)))/(Γ(1))) =((Γ((5/8))Γ((3/8)))/2)=(π/(2sin(((3π)/8))))=(π/(2cos(π/8)))=(π/(((√(2+(√2))))))
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt[{\mathrm{4}}]{{tanx}}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\frac{\mathrm{1}}{\mathrm{4}}} {x}\:{cos}^{−\frac{\mathrm{1}}{\mathrm{4}}} {x}\:{dx}\:\:\:\:\:\:\:\:{sin}^{\mathrm{2}} {x}={t}\Rightarrow{sin}\mathrm{2}{x}=\frac{{dt}}{{dx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{t}\right)^{−\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}} \:{dt}\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}}\right)}{\Gamma\left(\mathrm{1}\right)} \\ $$$$=\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{8}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{8}}\right)}{\mathrm{2}}=\frac{\pi}{\mathrm{2}{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)}=\frac{\pi}{\mathrm{2}{cos}\frac{\pi}{\mathrm{8}}}=\frac{\pi}{\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\right)} \\ $$
Commented by mathmax by abdo last updated on 07/Dec/20
I=∫_0 ^(π/2) ^4 (√(tanx))dx we do the changement (tanx)^(1/4) =t ⇒tanx=t^4 ⇒ x=arctan(t^4 ) ⇒ I =∫_0 ^∞ ((t×(4t^3 ))/(1+t^8 ))dt =4∫_0 ^∞ (t^4 /(1+t^8 ))dt =_(t=u^(1/8) ) 4 ∫_0 ^∞ (u^(1/2) /(1+u))×(1/8) u^((1/8)−1) du =(1/2)∫_0 ^∞ (u^((1/2)+(1/8)−1) /(1+u))du =(1/2)∫_0 ^∞ (u^((5/8)−1) /(1+u))du =(1/2)×(π/(sin(((5π)/8))))=(π/(2sin((π/2)+(π/8)))) =(π/(2cos((π/8))))=(π/(2×((√(2+(√2)))/2))) =(π/( (√(2+(√2))))) ⇒I=(π/( (√(2+(√2)))))
$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:^{\mathrm{4}} \sqrt{\mathrm{tanx}}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\left(\mathrm{tanx}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} =\mathrm{t}\:\Rightarrow\mathrm{tanx}=\mathrm{t}^{\mathrm{4}} \:\Rightarrow \\ $$$$\mathrm{x}=\mathrm{arctan}\left(\mathrm{t}^{\mathrm{4}} \right)\:\Rightarrow\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{t}×\left(\mathrm{4t}^{\mathrm{3}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{8}} }\mathrm{dt}\:=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\mathrm{4}} }{\mathrm{1}+\mathrm{t}^{\mathrm{8}} }\mathrm{dt} \\ $$$$=_{\mathrm{t}=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{8}}} } \:\:\:\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+\mathrm{u}}×\frac{\mathrm{1}}{\mathrm{8}}\:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{8}}−\mathrm{1}} \:\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{8}}−\mathrm{1}} }{\mathrm{1}+\mathrm{u}}\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{u}^{\frac{\mathrm{5}}{\mathrm{8}}−\mathrm{1}} }{\mathrm{1}+\mathrm{u}}\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{sin}\left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right)}=\frac{\pi}{\mathrm{2sin}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}\right)} \\ $$$$=\frac{\pi}{\mathrm{2cos}\left(\frac{\pi}{\mathrm{8}}\right)}=\frac{\pi}{\mathrm{2}×\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}}\:=\frac{\pi}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}\:\Rightarrow\mathrm{I}=\frac{\pi}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}} \\ $$
Commented by Study last updated on 07/Dec/20
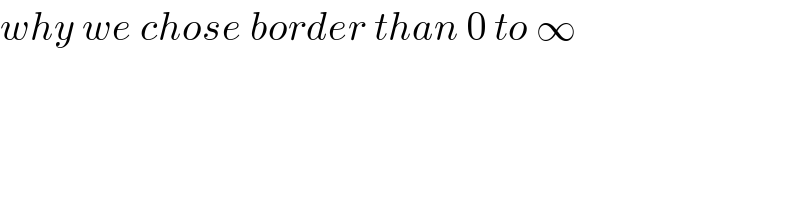
why we chose border than 0 to ∞
$${why}\:{we}\:{chose}\:{border}\:{than}\:\mathrm{0}\:{to}\:\infty \\ $$
Commented by Study last updated on 07/Dec/20
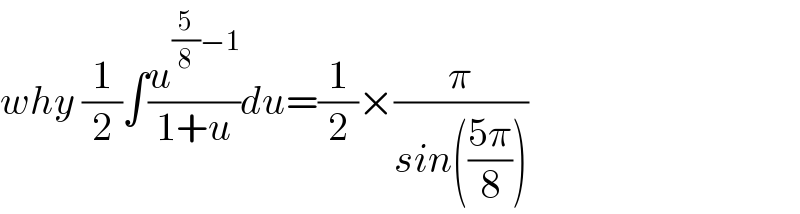
why (1/2)∫(u^((5/8)−1) /(1+u))du=(1/2)×(π/(sin(((5π)/8))))
$${why}\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{u}^{\frac{\mathrm{5}}{\mathrm{8}}−\mathrm{1}} }{\mathrm{1}+{u}}{du}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{{sin}\left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right)} \\ $$
Commented by Dwaipayan Shikari last updated on 07/Dec/20
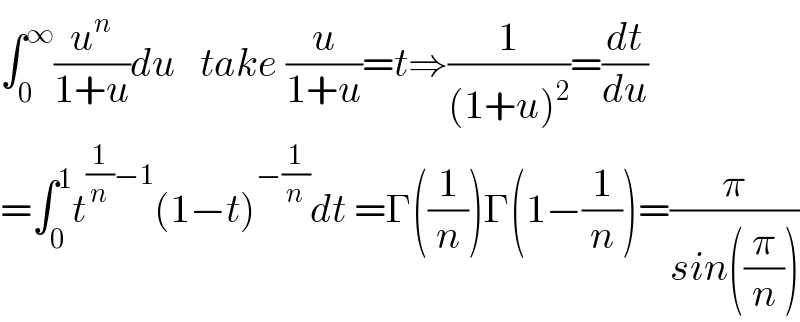
∫_0 ^∞ (u^n /(1+u))du take (u/(1+u))=t⇒(1/((1+u)^2 ))=(dt/du) =∫_0 ^1 t^((1/n)−1) (1−t)^(−(1/n)) dt =Γ((1/n))Γ(1−(1/n))=(π/(sin((π/n))))
$$\int_{\mathrm{0}} ^{\infty} \frac{{u}^{{n}} }{\mathrm{1}+{u}}{du}\:\:\:{take}\:\frac{{u}}{\mathrm{1}+{u}}={t}\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }=\frac{{dt}}{{du}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{−\frac{\mathrm{1}}{{n}}} {dt}\:=\Gamma\left(\frac{\mathrm{1}}{{n}}\right)\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)=\frac{\pi}{{sin}\left(\frac{\pi}{{n}}\right)} \\ $$
Commented by Bird last updated on 07/Dec/20
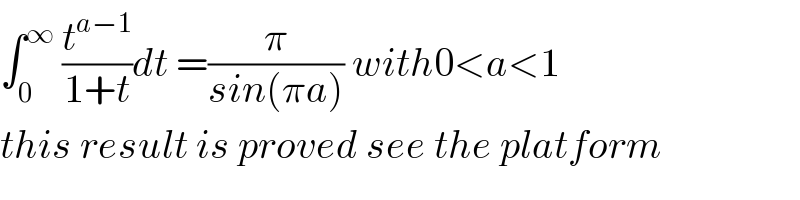
∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) with0<a<1 this result is proved see the platform
$$\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\frac{\pi}{{sin}\left(\pi{a}\right)}\:{with}\mathrm{0}<{a}<\mathrm{1} \\ $$$${this}\:{result}\:{is}\:{proved}\:{see}\:{the}\:{platform} \\ $$
Commented by Study last updated on 08/Dec/20
ans me please???
$${ans}\:{me}\:{please}??? \\ $$
Commented by Study last updated on 08/Dec/20
ans me please??
$${ans}\:{me}\:{please}?? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *