Question Number 124978 by rydasss last updated on 07/Dec/20

Answered by talminator2856791 last updated on 07/Dec/20
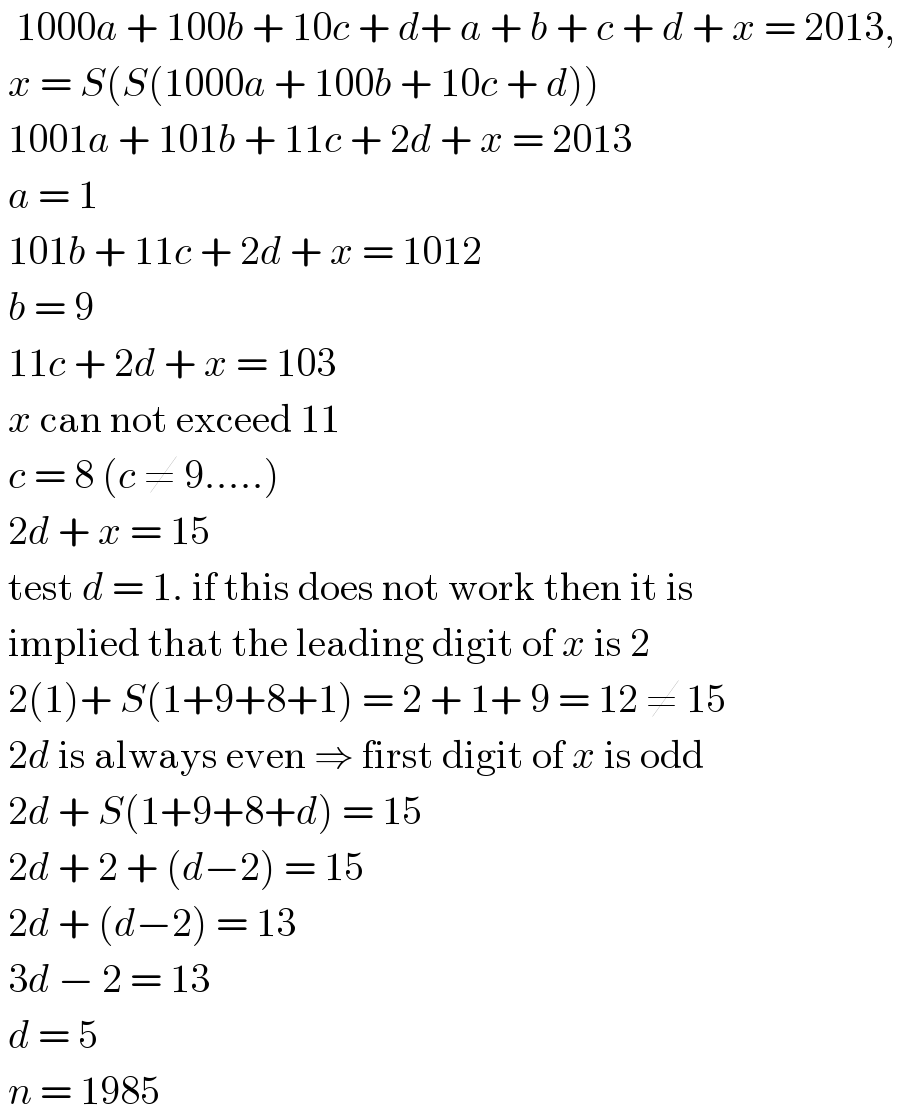
$$\:\:\mathrm{1000}{a}\:+\:\mathrm{100}{b}\:+\:\mathrm{10}{c}\:+\:{d}+\:{a}\:+\:{b}\:+\:{c}\:+\:{d}\:+\:{x}\:=\:\mathrm{2013},\:\: \\ $$$$\:{x}\:=\:{S}\left({S}\left(\mathrm{1000}{a}\:+\:\mathrm{100}{b}\:+\:\mathrm{10}{c}\:+\:{d}\right)\right) \\ $$$$\:\mathrm{1001}{a}\:+\:\mathrm{101}{b}\:+\:\mathrm{11}{c}\:+\:\mathrm{2}{d}\:+\:{x}\:=\:\mathrm{2013} \\ $$$$\:{a}\:=\:\mathrm{1} \\ $$$$\:\mathrm{101}{b}\:+\:\mathrm{11}{c}\:+\:\mathrm{2}{d}\:+\:{x}\:=\:\mathrm{1012} \\ $$$$\:{b}\:=\:\mathrm{9} \\ $$$$\:\mathrm{11}{c}\:+\:\mathrm{2}{d}\:+\:{x}\:=\:\mathrm{103} \\ $$$$\:{x}\:\mathrm{can}\:\mathrm{not}\:\mathrm{exceed}\:\mathrm{11} \\ $$$$\:{c}\:=\:\mathrm{8}\:\left({c}\:\neq\:\mathrm{9}…..\right) \\ $$$$\:\mathrm{2}{d}\:+\:{x}\:=\:\mathrm{15} \\ $$$$\:\mathrm{test}\:{d}\:=\:\mathrm{1}.\:\mathrm{if}\:\mathrm{this}\:\mathrm{does}\:\mathrm{not}\:\mathrm{work}\:\mathrm{then}\:\mathrm{it}\:\mathrm{is} \\ $$$$\:\mathrm{implied}\:\mathrm{that}\:\mathrm{the}\:\mathrm{leading}\:\mathrm{digit}\:\mathrm{of}\:{x}\:\mathrm{is}\:\mathrm{2} \\ $$$$\:\mathrm{2}\left(\mathrm{1}\right)+\:{S}\left(\mathrm{1}+\mathrm{9}+\mathrm{8}+\mathrm{1}\right)\:=\:\mathrm{2}\:+\:\mathrm{1}+\:\mathrm{9}\:=\:\mathrm{12}\:\neq\:\mathrm{15} \\ $$$$\:\mathrm{2}{d}\:\mathrm{is}\:\mathrm{always}\:\mathrm{even}\:\Rightarrow\:\mathrm{first}\:\mathrm{digit}\:\mathrm{of}\:{x}\:\mathrm{is}\:\mathrm{odd} \\ $$$$\:\mathrm{2}{d}\:+\:{S}\left(\mathrm{1}+\mathrm{9}+\mathrm{8}+{d}\right)\:=\:\mathrm{15} \\ $$$$\:\mathrm{2}{d}\:+\:\mathrm{2}\:+\:\left({d}−\mathrm{2}\right)\:=\:\mathrm{15} \\ $$$$\:\mathrm{2}{d}\:+\:\left({d}−\mathrm{2}\right)\:=\:\mathrm{13} \\ $$$$\:\mathrm{3}{d}\:−\:\mathrm{2}\:=\:\mathrm{13} \\ $$$$\:{d}\:=\:\mathrm{5} \\ $$$$\:{n}\:=\:\mathrm{1985} \\ $$
