Question Number 125108 by peter frank last updated on 08/Dec/20
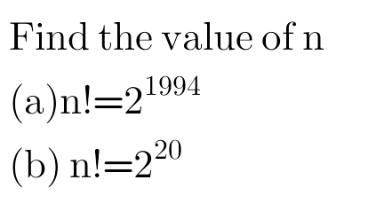
Commented by mr W last updated on 08/Dec/20

$${where}\:{did}\:{you}\:{get}\:{these}\:{questions}? \\ $$$${they}\:{are}\:{wrong},\:{i}.{e}.\:{there}\:{is}\:{no} \\ $$$${solution}. \\ $$$${the}\:{last}\:{digit}\:{of}\:\mathrm{2}^{{any}\:{integer}} \:{can}\:{only} \\ $$$${be}\:\mathrm{2},\mathrm{4},\mathrm{6},\mathrm{8}.\:{but}\:{the}\:{last}\:{digit}\:{of}\:{n}! \\ $$$${is}\:{always}\:\mathrm{0}\:{for}\:{n}\geqslant\mathrm{5}.\:{that}\:{means}: \\ $$$${n}!\neq\mathrm{2}^{{m}} \\ $$
Commented by MJS_new last updated on 08/Dec/20
$$\mathrm{maybe}\:\mathrm{the}\:\mathrm{usual}\:\mathrm{confusion}\:\mathrm{of}\:{n}!\:\mathrm{and}\:\Gamma\:\left({n}+\mathrm{1}\right) \\ $$
Commented by MJS_new last updated on 08/Dec/20

$$\left({a}\right)\:\mathrm{294}!<\mathrm{2}^{\mathrm{1994}} <\mathrm{295}! \\ $$$$\left({b}\right)\:\mathrm{9}!<\mathrm{2}^{\mathrm{20}} <\mathrm{10}! \\ $$
