Menu Close

Question-125173

Tinku Tara 0 Comments
Pin




Question Number 125173 by mohammad17 last updated on 08/Dec/20
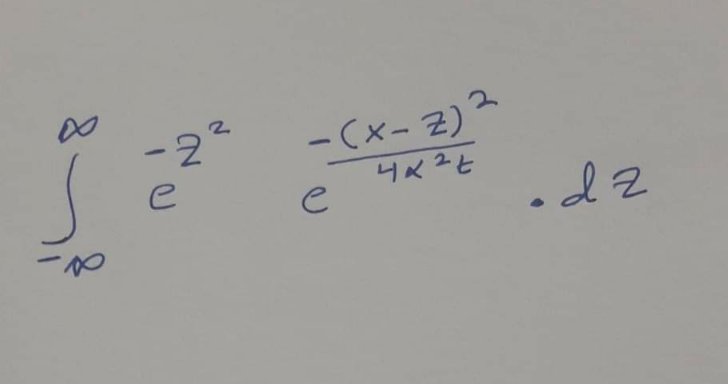
Commented by mohammad17 last updated on 08/Dec/20
please help me
$${please}\:{help}\:{me} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Dec/20
∫_(−∞) ^∞ e^(−z^2 −(((x−z)^2 )/(4α^2 t))) dz =∫_(−∞) ^∞ e^(−z^2 ((1/(4α^2 t))+1)+z((x/(2α^2 t)))−(x^2 /(4α^2 t))) dz =∫_(−∞) ^∞ e^(−((1/(4α^2 t))+1)((z−(x/( (1+4α^2 t))))^2 +(x^2 /(4α^2 t))−(x^2 /((1+4αt)^2 )))) dz =∫_(−∞) ^∞ e^(−((√((4α^2 t+1)/(4α^2 t)))(z−(x/((1+4α^2 t)))))^2 ) e^((−(x^2 /(4α^2 t))+(x^2 /((1+4αt)^2 )))((1/(4α^2 t))+1)) dz =2α(√((πt)/(4α^2 t+1))) e^(((x/((1+4α^2 t)))−(x^2 /(4α^2 t)))(((4α^2 t+1)/(4α^2 t)))) =2α(√((πt)/(4α^2 t+1))) e^((−x^2 )/(4α^2 t+1))
$$\int_{−\infty} ^{\infty} {e}^{−{z}^{\mathrm{2}} −\frac{\left({x}−{z}\right)^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} {t}}} {dz}\:\:\:\:\:\:\:\:\:\: \\ $$$$=\int_{−\infty} ^{\infty} {e}^{−{z}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}\alpha^{\mathrm{2}} {t}}+\mathrm{1}\right)+{z}\left(\frac{{x}}{\mathrm{2}\alpha^{\mathrm{2}} {t}}\right)−\frac{{x}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} {t}}} {dz} \\ $$$$=\int_{−\infty} ^{\infty} {e}^{−\left(\frac{\mathrm{1}}{\mathrm{4}\alpha^{\mathrm{2}} {t}}+\mathrm{1}\right)\left(\left({z}−\frac{{x}}{\:\left(\mathrm{1}+\mathrm{4}\alpha^{\mathrm{2}} {t}\right)}\right)^{\mathrm{2}} +\frac{{x}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} {t}}−\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{4}\alpha{t}\right)^{\mathrm{2}} }\right)} {dz} \\ $$$$=\int_{−\infty} ^{\infty} {e}^{−\left(\sqrt{\frac{\mathrm{4}\alpha^{\mathrm{2}} {t}+\mathrm{1}}{\mathrm{4}\alpha^{\mathrm{2}} {t}}}\left({z}−\frac{{x}}{\left(\mathrm{1}+\mathrm{4}\alpha^{\mathrm{2}} {t}\right)}\right)\right)^{\mathrm{2}} } {e}^{\left(−\frac{{x}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} {t}}+\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{4}\alpha{t}\right)^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}}{\mathrm{4}\alpha^{\mathrm{2}} {t}}+\mathrm{1}\right)} {dz} \\ $$$$=\mathrm{2}\alpha\sqrt{\frac{\pi{t}}{\mathrm{4}\alpha^{\mathrm{2}} {t}+\mathrm{1}}}\:{e}^{\left(\frac{{x}}{\left(\mathrm{1}+\mathrm{4}\alpha^{\mathrm{2}} {t}\right)}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} {t}}\right)\left(\frac{\mathrm{4}\alpha^{\mathrm{2}} {t}+\mathrm{1}}{\mathrm{4}\alpha^{\mathrm{2}} {t}}\right)} \\ $$$$=\mathrm{2}\alpha\sqrt{\frac{\pi{t}}{\mathrm{4}\alpha^{\mathrm{2}} {t}+\mathrm{1}}}\:{e}^{\frac{−{x}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} {t}+\mathrm{1}}} \\ $$
Commented by mohammad17 last updated on 08/Dec/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 08/Dec/20
i suppose that we have 3 parametr in this integral x ,α ant I(xαt) =∫_(−∞) ^(+∞) e^(−(z^2 +(((x−z)^2 )/(4α^2 t)))) dz =∫_(−∞) ^(+∞) e^(−{((4α^2 tz^2 +z^2 −2xz +x^2 )/(4α^2 t))}) dz =∫_(−∞) ^(+∞) e^(−{ (((4α^2 t+1)z^2 −2xz+x^2 )/(4α^2 t))}) dz but (4α^2 t +1)z^2 −2xz +x^2 =(4α^2 t+1){z^2 −((2x)/(4α^2 t +1))z +(x^2 /(4α^2 t +1))} =_(m=4α^2 t+1) m{z^2 −((2x)/m)z +(x^2 /m)} =m{z^2 −2(x/m)z +(x^2 /m^2 )+(x^2 /m)−(x^2 /m^2 )} =m{(z−(x/m))^2 +(((m−1)x^2 )/m^2 )} ⇒ I(x,α,t) =∫_(−∞) ^(+∞) e^(−((1m)/(4α^2 t)){(z−(x/m))^2 +(((m−1)x^2 )/m^2 )}) dz =∫_(−∞) ^(+∞) e^(−((√(m/(4α^2 t)))(z−(x/m)))^2 ) ×e^(−(((m−1)x^2 )/(4mα^2 t))) dz =_((√(m/(4α^2 t)))(z−(x/m))=w) e^(−(((m−1)x^2 )/(4mα^2 t))) ∫_(−∞) ^(+∞) e^(−w^2 ) (dw/( (√(m/(4α^2 t))))) =((m/(4α^2 t)))^(−(1/2)) (√π)× e^(−(((m−1)x^2 )/(4mα^2 t))) =(√π)(((4α^2 t+1)/(4α^2 t)))^(−(1/2)) ×e^(−(((4α^2 t+1−1)x^2 )/(4α^2 t(4α^2 t +1)))) =(√π)(1+(1/(4α^2 t)))^(−(1/2)) . e^(−(x^2 /(4α^2 t+1)))
$$\mathrm{i}\:\mathrm{suppose}\:\mathrm{that}\:\mathrm{we}\:\mathrm{have}\:\mathrm{3}\:\mathrm{parametr}\:\mathrm{in}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{x}\:,\alpha\:\mathrm{ant} \\ $$$$\mathrm{I}\left(\mathrm{x}\alpha\mathrm{t}\right)\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\left(\mathrm{z}^{\mathrm{2}} \:+\frac{\left(\mathrm{x}−\mathrm{z}\right)^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}}\right)} \mathrm{dz}\:\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\left\{\frac{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{tz}^{\mathrm{2}} \:+\mathrm{z}^{\mathrm{2}} −\mathrm{2xz}\:+\mathrm{x}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}}\right\}} \mathrm{dz} \\ $$$$=\int_{−\infty} ^{+\infty} \:\:\mathrm{e}^{−\left\{\:\:\frac{\left(\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}+\mathrm{1}\right)\mathrm{z}^{\mathrm{2}} −\mathrm{2xz}+\mathrm{x}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}}\right\}} \mathrm{dz}\:\:\mathrm{but} \\ $$$$\left(\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}\:+\mathrm{1}\right)\mathrm{z}^{\mathrm{2}} −\mathrm{2xz}\:+\mathrm{x}^{\mathrm{2}} \:=\left(\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}+\mathrm{1}\right)\left\{\mathrm{z}^{\mathrm{2}} \:−\frac{\mathrm{2x}}{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}\:+\mathrm{1}}\mathrm{z}\:+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}\:+\mathrm{1}}\right\} \\ $$$$=_{\mathrm{m}=\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}+\mathrm{1}} \:\:\:\mathrm{m}\left\{\mathrm{z}^{\mathrm{2}} −\frac{\mathrm{2x}}{\mathrm{m}}\mathrm{z}\:+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{m}}\right\}\:=\mathrm{m}\left\{\mathrm{z}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{x}}{\mathrm{m}}\mathrm{z}\:+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{m}^{\mathrm{2}} }+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{m}}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{m}^{\mathrm{2}} }\right\} \\ $$$$=\mathrm{m}\left\{\left(\mathrm{z}−\frac{\mathrm{x}}{\mathrm{m}}\right)^{\mathrm{2}} \:+\frac{\left(\mathrm{m}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} }{\mathrm{m}^{\mathrm{2}} }\right\}\:\Rightarrow \\ $$$$\mathrm{I}\left(\mathrm{x},\alpha,\mathrm{t}\right)\:=\int_{−\infty} ^{+\infty} \:\:\mathrm{e}^{−\frac{\mathrm{1m}}{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}}\left\{\left(\mathrm{z}−\frac{\mathrm{x}}{\mathrm{m}}\right)^{\mathrm{2}} \:+\frac{\left(\mathrm{m}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} }{\mathrm{m}^{\mathrm{2}} }\right\}} \mathrm{dz} \\ $$$$=\int_{−\infty} ^{+\infty} \:\:\:\mathrm{e}^{−\left(\sqrt{\frac{\mathrm{m}}{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}}}\left(\mathrm{z}−\frac{\mathrm{x}}{\mathrm{m}}\right)\right)^{\mathrm{2}} } ×\mathrm{e}^{−\frac{\left(\mathrm{m}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} }{\mathrm{4m}\alpha^{\mathrm{2}} \mathrm{t}}} \mathrm{dz} \\ $$$$=_{\sqrt{\frac{\mathrm{m}}{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}}}\left(\mathrm{z}−\frac{\mathrm{x}}{\mathrm{m}}\right)=\mathrm{w}} \:\:\:\:\mathrm{e}^{−\frac{\left(\mathrm{m}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} }{\mathrm{4m}\alpha^{\mathrm{2}} \mathrm{t}}} \:\:\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{w}^{\mathrm{2}} } \frac{\mathrm{dw}}{\:\sqrt{\frac{\mathrm{m}}{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}}}}\:\:\: \\ $$$$=\left(\frac{\mathrm{m}}{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\pi}×\:\mathrm{e}^{−\frac{\left(\mathrm{m}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} }{\mathrm{4m}\alpha^{\mathrm{2}} \mathrm{t}}} \\ $$$$=\sqrt{\pi}\left(\frac{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}+\mathrm{1}}{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} ×\mathrm{e}^{−\frac{\left(\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}+\mathrm{1}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}\left(\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}\:+\mathrm{1}\right)}} \\ $$$$=\sqrt{\pi}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:.\:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} \mathrm{t}+\mathrm{1}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *