Question Number 125186 by Mathgreat last updated on 08/Dec/20
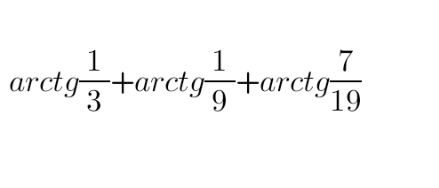
Answered by bemath last updated on 08/Dec/20
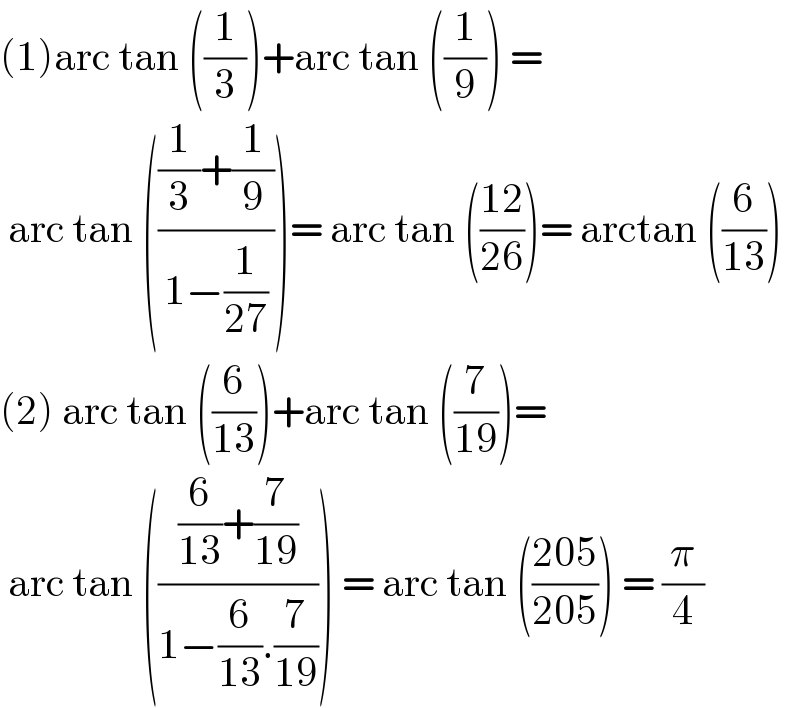
$$\left(\mathrm{1}\right)\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{1}}{\mathrm{9}}\right)\:= \\ $$$$\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{9}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{27}}}\right)=\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{12}}{\mathrm{26}}\right)=\:\mathrm{arctan}\:\left(\frac{\mathrm{6}}{\mathrm{13}}\right) \\ $$$$\left(\mathrm{2}\right)\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{6}}{\mathrm{13}}\right)+\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{7}}{\mathrm{19}}\right)= \\ $$$$\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\frac{\mathrm{6}}{\mathrm{13}}+\frac{\mathrm{7}}{\mathrm{19}}}{\mathrm{1}−\frac{\mathrm{6}}{\mathrm{13}}.\frac{\mathrm{7}}{\mathrm{19}}}\right)\:=\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{205}}{\mathrm{205}}\right)\:=\:\frac{\pi}{\mathrm{4}} \\ $$
