Question Number 125195 by Eric002 last updated on 09/Dec/20

Answered by mr W last updated on 09/Dec/20

$$\frac{{AD}}{\mathrm{sin}\:\mathrm{58}}=\frac{{DC}}{\mathrm{sin}\:{x}}\:\:\:…\left({i}\right) \\ $$$$\frac{{AD}}{\mathrm{sin}\:\angle{B}}=\frac{{BD}}{\mathrm{sin}\:\mathrm{32}}\: \\ $$$$\angle{B}=\mathrm{180}−\mathrm{58}−{x}+\mathrm{32}=\mathrm{90}−{x} \\ $$$$\frac{{AD}}{\mathrm{cos}\:{x}}=\frac{{DC}}{\mathrm{sin}\:\mathrm{32}}\:\:\:…\left({ii}\right) \\ $$$$\left({ii}\right)\boldsymbol{\div}\left({i}\right): \\ $$$$\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:\mathrm{58}}=\frac{\mathrm{sin}\:\mathrm{32}}{\mathrm{sin}\:{x}} \\ $$$$\Rightarrow\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}=\mathrm{sin}\:\mathrm{32}\:\mathrm{cos}\:\mathrm{32}=\mathrm{sin}\:\mathrm{58}\:\mathrm{cos}\:\mathrm{58} \\ $$$$\Rightarrow{x}=\mathrm{32}°\:{or}\:\mathrm{58}° \\ $$
Commented by Eric002 last updated on 09/Dec/20

$${well}\:{done} \\ $$
Commented by mr W last updated on 09/Dec/20
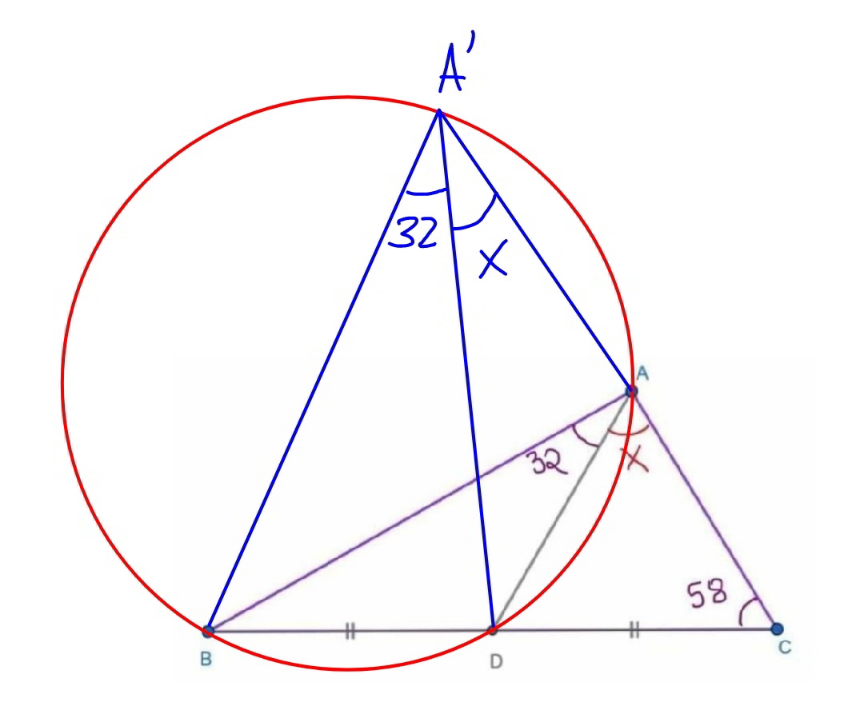
Commented by mr W last updated on 09/Dec/20

$${this}\:{shows}\:{why}\:{two}\:{solutions}\:{exist}. \\ $$
