Question Number 125199 by joki last updated on 09/Dec/20

Answered by bemath last updated on 09/Dec/20
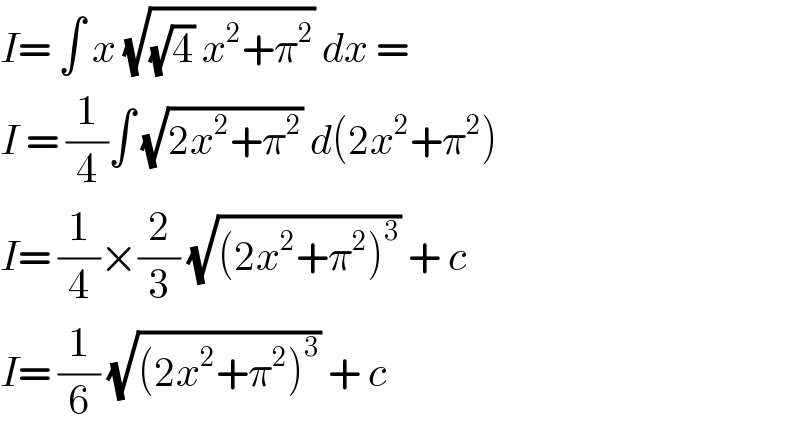
$${I}=\:\int\:{x}\:\sqrt{\sqrt{\mathrm{4}}\:{x}^{\mathrm{2}} +\pi^{\mathrm{2}} }\:{dx}\:=\: \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\int\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\pi^{\mathrm{2}} }\:{d}\left(\mathrm{2}{x}^{\mathrm{2}} +\pi^{\mathrm{2}} \right) \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{2}}{\mathrm{3}}\:\sqrt{\left(\mathrm{2}{x}^{\mathrm{2}} +\pi^{\mathrm{2}} \right)^{\mathrm{3}} }\:+\:{c} \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{6}}\:\sqrt{\left(\mathrm{2}{x}^{\mathrm{2}} +\pi^{\mathrm{2}} \right)^{\mathrm{3}} }\:+\:{c}\: \\ $$
