Question Number 125230 by mohammad17 last updated on 09/Dec/20
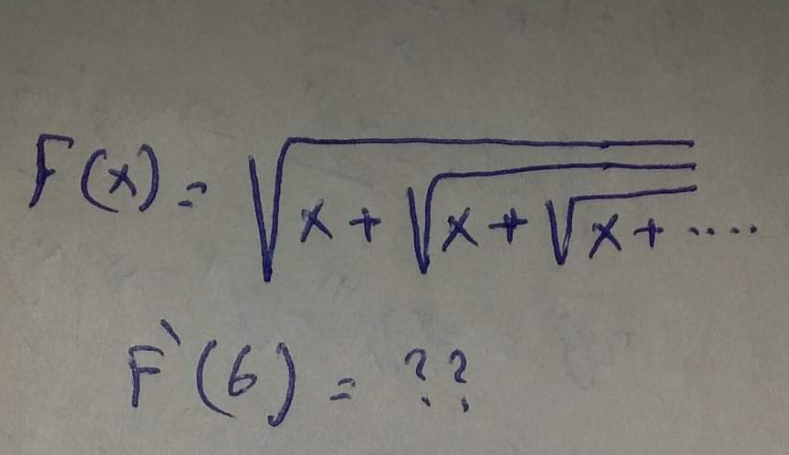
Answered by mathmax by abdo last updated on 09/Dec/20
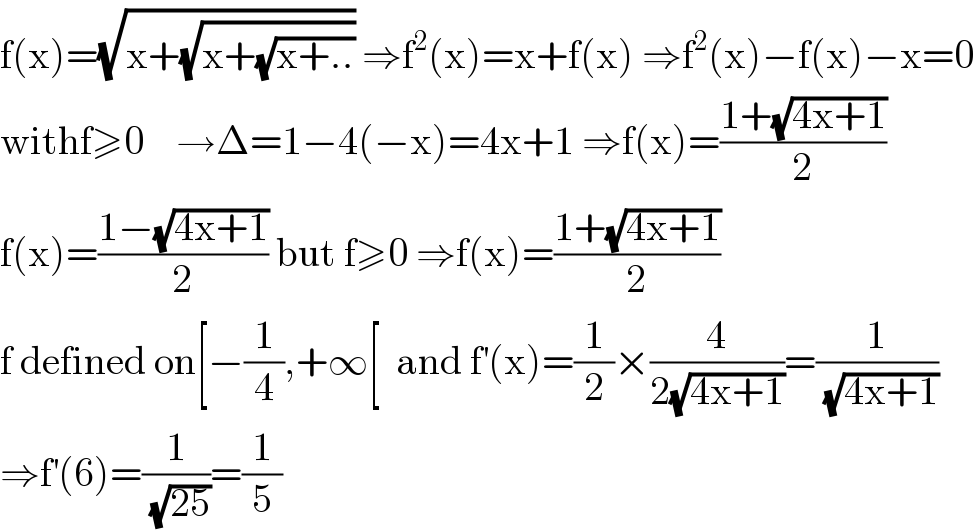
$$\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+..}}}\:\Rightarrow\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{x}+\mathrm{f}\left(\mathrm{x}\right)\:\Rightarrow\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{x}\right)−\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{withf}\geqslant\mathrm{0}\:\:\:\:\rightarrow\Delta=\mathrm{1}−\mathrm{4}\left(−\mathrm{x}\right)=\mathrm{4x}+\mathrm{1}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{4x}+\mathrm{1}}}{\mathrm{2}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}−\sqrt{\mathrm{4x}+\mathrm{1}}}{\mathrm{2}}\:\mathrm{but}\:\mathrm{f}\geqslant\mathrm{0}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{4x}+\mathrm{1}}}{\mathrm{2}} \\ $$$$\mathrm{f}\:\mathrm{defined}\:\mathrm{on}\left[−\frac{\mathrm{1}}{\mathrm{4}},+\infty\left[\:\:\mathrm{and}\:\mathrm{f}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{4x}+\mathrm{1}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{4x}+\mathrm{1}}}\right.\right. \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{6}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{25}}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$
