Question Number 125263 by mohammad17 last updated on 09/Dec/20

Commented by mohammad17 last updated on 09/Dec/20

$${help}\:{me}\:{sir} \\ $$
Answered by Olaf last updated on 09/Dec/20
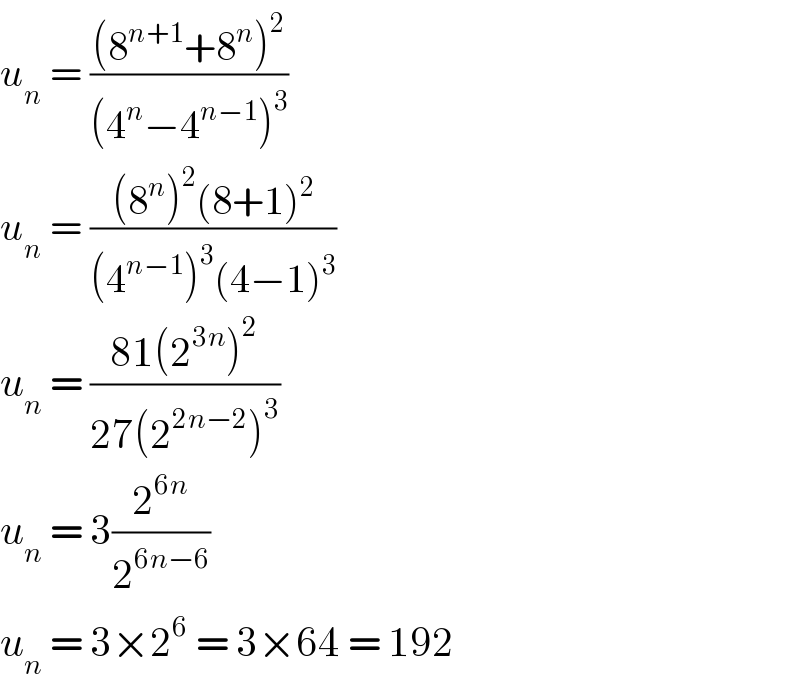
$${u}_{{n}} \:=\:\frac{\left(\mathrm{8}^{{n}+\mathrm{1}} +\mathrm{8}^{{n}} \right)^{\mathrm{2}} }{\left(\mathrm{4}^{{n}} −\mathrm{4}^{{n}−\mathrm{1}} \right)^{\mathrm{3}} } \\ $$$${u}_{{n}} \:=\:\frac{\left(\mathrm{8}^{{n}} \right)^{\mathrm{2}} \left(\mathrm{8}+\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{4}^{{n}−\mathrm{1}} \right)^{\mathrm{3}} \left(\mathrm{4}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${u}_{{n}} \:=\:\frac{\mathrm{81}\left(\mathrm{2}^{\mathrm{3}{n}} \right)^{\mathrm{2}} }{\mathrm{27}\left(\mathrm{2}^{\mathrm{2}{n}−\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$${u}_{{n}} \:=\:\mathrm{3}\frac{\mathrm{2}^{\mathrm{6}{n}} }{\mathrm{2}^{\mathrm{6}{n}−\mathrm{6}} } \\ $$$${u}_{{n}} \:=\:\mathrm{3}×\mathrm{2}^{\mathrm{6}} \:=\:\mathrm{3}×\mathrm{64}\:=\:\mathrm{192} \\ $$
Commented by mohammad17 last updated on 10/Dec/20

$${thank}\:{you}\:{sir} \\ $$
