Question Number 125264 by mohammad17 last updated on 09/Dec/20
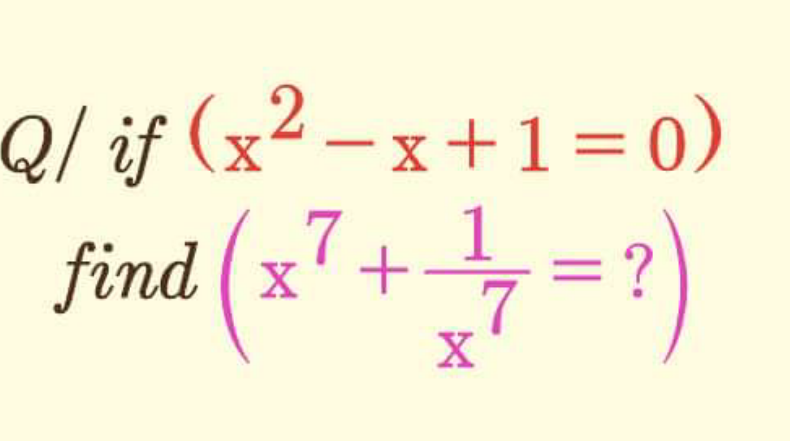
Answered by Ar Brandon last updated on 09/Dec/20
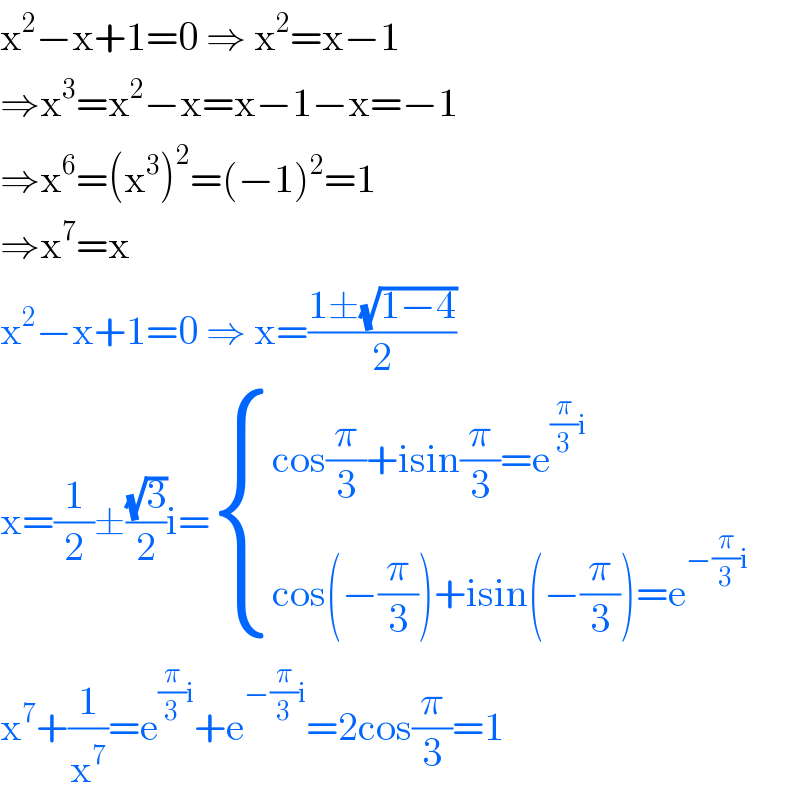
$$\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:\mathrm{x}^{\mathrm{2}} =\mathrm{x}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{3}} =\mathrm{x}^{\mathrm{2}} −\mathrm{x}=\mathrm{x}−\mathrm{1}−\mathrm{x}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{6}} =\left(\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{2}} =\left(−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{7}} =\mathrm{x} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:\mathrm{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}}}{\mathrm{2}} \\ $$$$\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}=\begin{cases}{\mathrm{cos}\frac{\pi}{\mathrm{3}}+\mathrm{isin}\frac{\pi}{\mathrm{3}}=\mathrm{e}^{\frac{\pi}{\mathrm{3}}\mathrm{i}} }\\{\mathrm{cos}\left(−\frac{\pi}{\mathrm{3}}\right)+\mathrm{isin}\left(−\frac{\pi}{\mathrm{3}}\right)=\mathrm{e}^{−\frac{\pi}{\mathrm{3}}\mathrm{i}} }\end{cases} \\ $$$$\mathrm{x}^{\mathrm{7}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{7}} }=\mathrm{e}^{\frac{\pi}{\mathrm{3}}\mathrm{i}} +\mathrm{e}^{−\frac{\pi}{\mathrm{3}}\mathrm{i}} =\mathrm{2cos}\frac{\pi}{\mathrm{3}}=\mathrm{1} \\ $$
Commented by mohammad17 last updated on 10/Dec/20
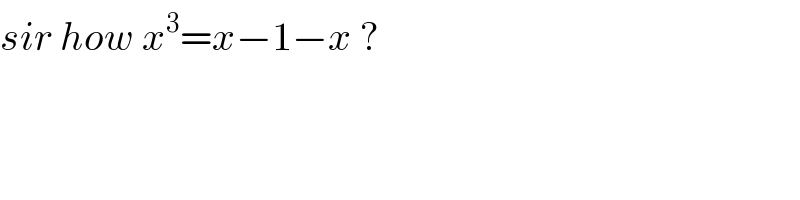
$${sir}\:{how}\:{x}^{\mathrm{3}} ={x}−\mathrm{1}−{x}\:? \\ $$
Commented by Ar Brandon last updated on 10/Dec/20
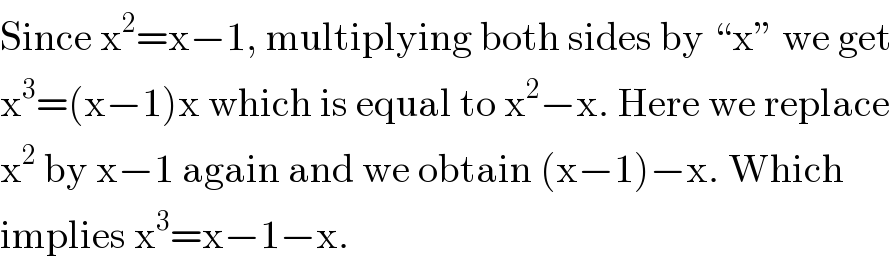
$$\mathrm{Since}\:\mathrm{x}^{\mathrm{2}} =\mathrm{x}−\mathrm{1},\:\mathrm{multiplying}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{by}\:“\mathrm{x}''\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}^{\mathrm{3}} =\left(\mathrm{x}−\mathrm{1}\right)\mathrm{x}\:\mathrm{which}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}.\:\mathrm{Here}\:\mathrm{we}\:\mathrm{replace} \\ $$$$\mathrm{x}^{\mathrm{2}} \:\mathrm{by}\:\mathrm{x}−\mathrm{1}\:\mathrm{again}\:\mathrm{and}\:\mathrm{we}\:\mathrm{obtain}\:\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{x}.\:\mathrm{Which} \\ $$$$\mathrm{implies}\:\mathrm{x}^{\mathrm{3}} =\mathrm{x}−\mathrm{1}−\mathrm{x}. \\ $$
Answered by Dwaipayan Shikari last updated on 10/Dec/20
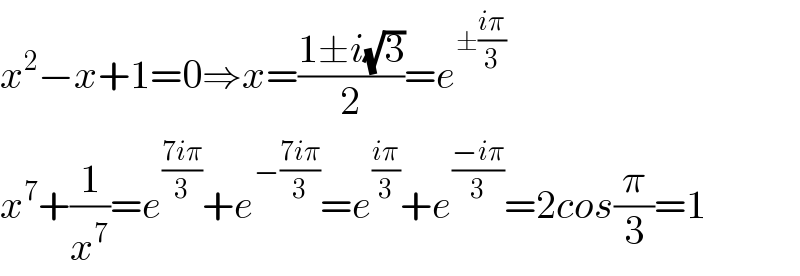
$${x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{\pm\frac{{i}\pi}{\mathrm{3}}} \\ $$$${x}^{\mathrm{7}} +\frac{\mathrm{1}}{{x}^{\mathrm{7}} }={e}^{\frac{\mathrm{7}{i}\pi}{\mathrm{3}}} +{e}^{−\frac{\mathrm{7}{i}\pi}{\mathrm{3}}} ={e}^{\frac{{i}\pi}{\mathrm{3}}} +{e}^{\frac{−{i}\pi}{\mathrm{3}}} =\mathrm{2}{cos}\frac{\pi}{\mathrm{3}}=\mathrm{1} \\ $$
