Question-125295

Question Number 125295 by mr W last updated on 09/Dec/20

Commented by mr W last updated on 09/Dec/20

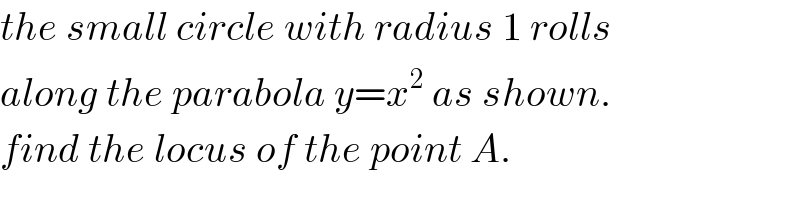
the small circle with radius 1 rolls along the parabola y=x^2 as shown. find the locus of the point A.

$${the}\:{small}\:{circle}\:{with}\:{radius}\:\mathrm{1}\:{rolls} \\ $$$${along}\:{the}\:{parabola}\:{y}={x}^{\mathrm{2}} \:{as}\:{shown}. \\ $$$${find}\:{the}\:{locus}\:{of}\:{the}\:{point}\:{A}. \\ $$

Answered by Olaf last updated on 09/Dec/20

Let M(t) = (((x(t) = t)),((y(t) = t^2 )) ) l(t) = ∫_0 ^t (√(x′^2 (τ)+y′^2 (τ)))dτ l(t) = ∫_0 ^t (√(1+4τ^2 ))dτ Let τ = (1/2)sinhϕ l(t) = ∫_0 ^(argsh(2t)) (√(1+sinh^2 ϕ)).(1/2)coshϕdϕ l(t) = ∫_0 ^(argsh(2t)) (1/2)cosh^2 ϕdϕ l(t) = ∫_0 ^(argsh(2t)) ((1+cosh(2ϕ))/4)dϕ l(t) = (1/4)[ϕ+(1/2)sinh(2ϕ)]_0 ^(argsh(2t)) l(t) = (1/4)[ϕ+sinhϕcoshϕ]_0 ^(argsh(2t)) l(t) = (1/4)(argsh(2t)+2t(√(1+4t^2 ))) l(t) = (1/4)[ln(2t+(√(1+4t^2 )))+2t(√(1+4t^2 ))] OA^(→) (t) = OM^(→) (t)+MA^(→) (t) OA^(→) (t) = ((t),(t^2 ) )+ (((rcos(θ(t)))),((rsin(θ(t)))) ) r = 1 and : l(t) = rθ(t) = θ(t) OA^(→) (t) = (((t+cos[(1/4)(ln(2t+(√(1+4t^2 )))+2t(√(1+4t^2 )))])),((t^2 +sin[(1/4)(ln(2t+(√(1+4t^2 )))+2t(√(1+4t^2 )))])) )

$$\mathrm{Let}\:\mathrm{M}\left({t}\right)\:=\:\begin{pmatrix}{{x}\left({t}\right)\:=\:{t}}\\{{y}\left({t}\right)\:=\:{t}^{\mathrm{2}} }\end{pmatrix} \\ $$$${l}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{{t}} \sqrt{{x}'^{\mathrm{2}} \left(\tau\right)+{y}'^{\mathrm{2}} \left(\tau\right)}{d}\tau \\ $$$${l}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{{t}} \sqrt{\mathrm{1}+\mathrm{4}\tau^{\mathrm{2}} }{d}\tau \\ $$$$\mathrm{Let}\:\tau\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinh}\varphi \\ $$$${l}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{2}{t}\right)} \sqrt{\mathrm{1}+\mathrm{sinh}^{\mathrm{2}} \varphi}.\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cosh}\varphi{d}\varphi \\ $$$${l}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{2}{t}\right)} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{cosh}^{\mathrm{2}} \varphi{d}\varphi \\ $$$${l}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{2}{t}\right)} \frac{\mathrm{1}+\mathrm{cosh}\left(\mathrm{2}\varphi\right)}{\mathrm{4}}{d}\varphi \\ $$$${l}\left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\varphi+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinh}\left(\mathrm{2}\varphi\right)\right]_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{2}{t}\right)} \\ $$$${l}\left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\varphi+\mathrm{sinh}\varphi\mathrm{cosh}\varphi\right]_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{2}{t}\right)} \\ $$$${l}\left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{argsh}\left(\mathrm{2}{t}\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right) \\ $$$${l}\left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\left(\mathrm{2}{t}+\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right] \\ $$$$\overset{\rightarrow} {\mathrm{OA}}\left({t}\right)\:=\:\overset{\rightarrow} {\mathrm{OM}}\left({t}\right)+\overset{\rightarrow} {\mathrm{MA}}\left({t}\right) \\ $$$$\overset{\rightarrow} {\mathrm{OA}}\left({t}\right)\:=\:\begin{pmatrix}{{t}}\\{{t}^{\mathrm{2}} }\end{pmatrix}+\begin{pmatrix}{{r}\mathrm{cos}\left(\theta\left({t}\right)\right)}\\{{r}\mathrm{sin}\left(\theta\left({t}\right)\right)}\end{pmatrix} \\ $$$${r}\:=\:\mathrm{1}\:\mathrm{and}\:: \\ $$$${l}\left({t}\right)\:=\:{r}\theta\left({t}\right)\:=\:\theta\left({t}\right) \\ $$$$\overset{\rightarrow} {\mathrm{OA}}\left({t}\right)\:=\:\begin{pmatrix}{{t}+\mathrm{cos}\left[\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{ln}\left(\mathrm{2}{t}+\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)\right]}\\{{t}^{\mathrm{2}} +\mathrm{sin}\left[\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{ln}\left(\mathrm{2}{t}+\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)\right]}\end{pmatrix} \\ $$

Answered by mr W last updated on 09/Dec/20

Commented by mr W last updated on 10/Dec/20

P(t,t^2 ) s=OP^(⌢) =∫_0 ^t (√(1+(2x)^2 ))dx =(1/4)[ln (2x+(√(1+4x^2 )))+2x(√(1+4x^2 ))]_0 ^t =(1/4)[ln (2t+(√(1+4t^2 )))+2t(√(1+4t^2 ))] s=PA^(⌢) =rϕ=1×ϕ ⇒ϕ=(1/4)[ln (2t+(√(1+4t^2 )))+2t(√(1+4t^2 ))] tan θ=(dy/dx)=2t ⇒sin θ=((2t)/( (√(1+4t^2 )))), cos θ=(1/( (√(1+4t^2 )))) rotation of circle: φ=θ+ϕ=tan^(−1) (2t)+(1/4)[ln (2t+(√(1+4t^2 )))+2t(√(1+4t^2 ))] x_A =t+1×sin θ−1×sin (θ+ϕ) =t+sin θ (1−cos ϕ)−cos θ sin ϕ =t+((2t)/( (√(1+4t^2 )))) (1−cos ϕ)−(1/( (√(1+4t^2 )))) sin ϕ y_A =t^2 −1×cos θ+1×cos (θ+ϕ) =t^2 −cos θ(1−cos ϕ)−sin θ sin ϕ =t^2 −(1/( (√(1+4t^2 ))))(1−cos ϕ)−((2t)/( (√(1+4t^2 ))))sin ϕ A: { ((x=t+((2t(1−cos ϕ)−sin ϕ)/( (√(1+4t^2 )))))),((y=t^2 −((1−cos ϕ+2t sin ϕ)/( (√(1+4t^2 )))))) :} general case: ϕ=(1/(4r))[ln (2t+(√(1+4t^2 )))+2t(√(1+4t^2 ))] x_A =t+((2t(r−l cos ϕ)− l sin ϕ)/( (√(1+4t^2 )))) y_A =t^2 −((r−l cos ϕ+ 2t l sin ϕ)/( (√(1+4t^2 ))))

$${P}\left({t},{t}^{\mathrm{2}} \right) \\ $$$${s}=\overset{\frown} {{OP}}=\int_{\mathrm{0}} ^{{t}} \sqrt{\mathrm{1}+\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\:\left(\mathrm{2}{x}+\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }\right)+\mathrm{2}{x}\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\:\left(\mathrm{2}{t}+\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right] \\ $$$${s}=\overset{\frown} {{PA}}={r}\varphi=\mathrm{1}×\varphi \\ $$$$\Rightarrow\varphi=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\:\left(\mathrm{2}{t}+\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right] \\ $$$$ \\ $$$$\mathrm{tan}\:\theta=\frac{{dy}}{{dx}}=\mathrm{2}{t}\: \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }},\:\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }} \\ $$$$ \\ $$$${rotation}\:{of}\:{circle}: \\ $$$$\phi=\theta+\varphi=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{t}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\:\left(\mathrm{2}{t}+\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right] \\ $$$$ \\ $$$${x}_{{A}} ={t}+\mathrm{1}×\mathrm{sin}\:\theta−\mathrm{1}×\mathrm{sin}\:\left(\theta+\varphi\right) \\ $$$$={t}+\mathrm{sin}\:\theta\:\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)−\mathrm{cos}\:\theta\:\mathrm{sin}\:\varphi \\ $$$$={t}+\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\:\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\:\mathrm{sin}\:\varphi \\ $$$$ \\ $$$${y}_{{A}} ={t}^{\mathrm{2}} −\mathrm{1}×\mathrm{cos}\:\theta+\mathrm{1}×\mathrm{cos}\:\left(\theta+\varphi\right) \\ $$$$={t}^{\mathrm{2}} −\mathrm{cos}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)−\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi \\ $$$$={t}^{\mathrm{2}} −\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)−\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\mathrm{sin}\:\varphi \\ $$$$ \\ $$$${A}:\begin{cases}{{x}={t}+\frac{\mathrm{2}{t}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)−\mathrm{sin}\:\varphi}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}}\\{{y}={t}^{\mathrm{2}} −\frac{\mathrm{1}−\mathrm{cos}\:\varphi+\mathrm{2}{t}\:\mathrm{sin}\:\varphi}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}}\end{cases} \\ $$$$ \\ $$$${general}\:{case}: \\ $$$$\varphi=\frac{\mathrm{1}}{\mathrm{4}{r}}\left[\mathrm{ln}\:\left(\mathrm{2}{t}+\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right)+\mathrm{2}{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\right] \\ $$$${x}_{{A}} ={t}+\frac{\mathrm{2}{t}\left({r}−{l}\:\mathrm{cos}\:\varphi\right)−\:{l}\:\mathrm{sin}\:\varphi}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }} \\ $$$${y}_{{A}} ={t}^{\mathrm{2}} −\frac{{r}−{l}\:\mathrm{cos}\:\varphi+\:\mathrm{2}{t}\:{l}\:\mathrm{sin}\:\varphi}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }} \\ $$

Commented by mr W last updated on 10/Dec/20