Question Number 125337 by ajfour last updated on 10/Dec/20

Commented by ajfour last updated on 10/Dec/20
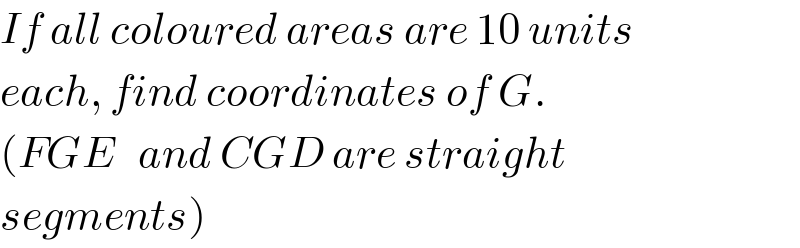
$${If}\:{all}\:{coloured}\:{areas}\:{are}\:\mathrm{10}\:{units} \\ $$$${each},\:{find}\:{coordinates}\:{of}\:{G}. \\ $$$$\left({FGE}\:\:\:{and}\:{CGD}\:{are}\:{straight}\right. \\ $$$$\left.{segments}\right) \\ $$
Answered by ajfour last updated on 10/Dec/20
![let G(p,q) , C(0,c) , F(0, f) eq. of AB : x+y=10 E(2p, 2q−f) ⇒ 2p+2q−f=10 ...(i) D(d, 0) (q/(d−p))=(c/d) ....(ii) p(c−f)=20 ...(iii) (10−c)(2p)=20 ....(iv) cd=40 ....(v) ⇒ q=(c^2 /(40))(((40)/c)−p) ....(I) f=c−((20)/p) 2p+(c^2 /(20))(((40)/c)−p)=10+c−((20)/p) ..(II) from (iv) c=10−((10)/p) substituting for c in (II) 2p+10−((10)/p)−(p/(20))(10−((10)/p))^2 =10−((20)/p) ⇒ 2p+((10)/p)−5p(1−(2/p)+(1/p^2 ))=0 ⇒ 2p+((10)/p)−5p+10−(5/p)=0 ⇒ 3p−(5/p)=10 ⇒ 3p^2 −10p−5 = 0 p=(5/3)+(√(((25)/9)+((15)/9))) p=((5+2(√(10)))/3) c=10(1−(3/(5+2(√(10)))))=10(((2+2(√(10)))/(5+2(√(10))))) =4(1+(√(10)))(2(√(10))−5)/3 =(4/3)(2(√(10))−5+20−5(√(10))) c =4(5−(√(10))) And from (I) : q=(c^2 /(40))(((40)/c)−p) q= c−((c^2 p)/(40)) =20−4(√(10))−((16(5−(√(10)))^2 (5+2(√(10))))/(40×3)) q= 20−4(√(10))−((2(7−2(√(10)))(5+2(√(10))))/3) =((60−12(√(10))−2(7−2(√(10)))(5+2(√(10))))/3) =((60−12(√(10))−2(35+14(√(10))−10(√(10))−40))/3) =((70−20(√(10)))/3) = ((10)/3)(7−2(√(10))) G[((5+2(√(10)))/3) , ((10)/3)(7−2(√(10)) )] .](https://www.tinkutara.com/question/Q125351.png)
$${let}\:\:{G}\left({p},{q}\right)\:\:,\:\:{C}\left(\mathrm{0},{c}\right)\:\:,\:\:{F}\left(\mathrm{0},\:{f}\right) \\ $$$${eq}.\:{of}\:{AB}\::\:\:\:\:{x}+{y}=\mathrm{10} \\ $$$${E}\left(\mathrm{2}{p},\:\mathrm{2}{q}−{f}\right) \\ $$$$\Rightarrow\:\:\:\mathrm{2}{p}+\mathrm{2}{q}−{f}=\mathrm{10}\:\:\:\:\:\:\:…\left({i}\right) \\ $$$${D}\left({d},\:\mathrm{0}\right) \\ $$$$\frac{{q}}{{d}−{p}}=\frac{{c}}{{d}}\:\:\:\:\:\:….\left({ii}\right) \\ $$$${p}\left({c}−{f}\right)=\mathrm{20}\:\:\:\:\:\:…\left({iii}\right) \\ $$$$\left(\mathrm{10}−{c}\right)\left(\mathrm{2}{p}\right)=\mathrm{20}\:\:\:\:\:….\left({iv}\right) \\ $$$$\:\:\:\:\:\:\:{cd}=\mathrm{40}\:\:\:\:\:\:\:\:\:\:\:….\left({v}\right) \\ $$$$\Rightarrow\:\:\:{q}=\frac{{c}^{\mathrm{2}} }{\mathrm{40}}\left(\frac{\mathrm{40}}{{c}}−{p}\right)\:\:\:\:….\left({I}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{f}={c}−\frac{\mathrm{20}}{{p}} \\ $$$$\:\:\:\:\mathrm{2}{p}+\frac{{c}^{\mathrm{2}} }{\mathrm{20}}\left(\frac{\mathrm{40}}{{c}}−{p}\right)=\mathrm{10}+{c}−\frac{\mathrm{20}}{{p}}\:\:\:..\left({II}\right) \\ $$$${from}\:\:\left({iv}\right) \\ $$$$\:\:\:{c}=\mathrm{10}−\frac{\mathrm{10}}{{p}} \\ $$$$\:\:\:{substituting}\:{for}\:{c}\:{in}\:\left({II}\right) \\ $$$$\:\:\mathrm{2}{p}+\mathrm{10}−\frac{\mathrm{10}}{{p}}−\frac{{p}}{\mathrm{20}}\left(\mathrm{10}−\frac{\mathrm{10}}{{p}}\right)^{\mathrm{2}} =\mathrm{10}−\frac{\mathrm{20}}{{p}} \\ $$$$\Rightarrow\:\:\mathrm{2}{p}+\frac{\mathrm{10}}{{p}}−\mathrm{5}{p}\left(\mathrm{1}−\frac{\mathrm{2}}{{p}}+\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{2}{p}+\frac{\mathrm{10}}{{p}}−\mathrm{5}{p}+\mathrm{10}−\frac{\mathrm{5}}{{p}}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{3}{p}−\frac{\mathrm{5}}{{p}}=\mathrm{10} \\ $$$$\Rightarrow\:\:\:\:\mathrm{3}{p}^{\mathrm{2}} −\mathrm{10}{p}−\mathrm{5}\:=\:\mathrm{0} \\ $$$${p}=\frac{\mathrm{5}}{\mathrm{3}}+\sqrt{\frac{\mathrm{25}}{\mathrm{9}}+\frac{\mathrm{15}}{\mathrm{9}}} \\ $$$$\:\:\:\:{p}=\frac{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{10}}}{\mathrm{3}}\:\:\: \\ $$$$\:\:\:{c}=\mathrm{10}\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{10}}}\right)=\mathrm{10}\left(\frac{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{10}}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{10}}}\right) \\ $$$$\:\:\:\:\:=\mathrm{4}\left(\mathrm{1}+\sqrt{\mathrm{10}}\right)\left(\mathrm{2}\sqrt{\mathrm{10}}−\mathrm{5}\right)/\mathrm{3} \\ $$$$\:\:\:\:\:=\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{2}\sqrt{\mathrm{10}}−\mathrm{5}+\mathrm{20}−\mathrm{5}\sqrt{\mathrm{10}}\right) \\ $$$$\:\:{c}\:=\mathrm{4}\left(\mathrm{5}−\sqrt{\mathrm{10}}\right) \\ $$$$\:{And}\:{from}\:\left({I}\right)\::\:\:{q}=\frac{{c}^{\mathrm{2}} }{\mathrm{40}}\left(\frac{\mathrm{40}}{{c}}−{p}\right) \\ $$$$\:\:{q}=\:{c}−\frac{{c}^{\mathrm{2}} {p}}{\mathrm{40}}\: \\ $$$$\:=\mathrm{20}−\mathrm{4}\sqrt{\mathrm{10}}−\frac{\mathrm{16}\left(\mathrm{5}−\sqrt{\mathrm{10}}\right)^{\mathrm{2}} \left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{10}}\right)}{\mathrm{40}×\mathrm{3}} \\ $$$$\:{q}=\:\mathrm{20}−\mathrm{4}\sqrt{\mathrm{10}}−\frac{\mathrm{2}\left(\mathrm{7}−\mathrm{2}\sqrt{\mathrm{10}}\right)\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{10}}\right)}{\mathrm{3}} \\ $$$$\:\:=\frac{\mathrm{60}−\mathrm{12}\sqrt{\mathrm{10}}−\mathrm{2}\left(\mathrm{7}−\mathrm{2}\sqrt{\mathrm{10}}\right)\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{10}}\right)}{\mathrm{3}} \\ $$$$\:\:=\frac{\mathrm{60}−\mathrm{12}\sqrt{\mathrm{10}}−\mathrm{2}\left(\mathrm{35}+\mathrm{14}\sqrt{\mathrm{10}}−\mathrm{10}\sqrt{\mathrm{10}}−\mathrm{40}\right)}{\mathrm{3}} \\ $$$$\:\:=\frac{\mathrm{70}−\mathrm{20}\sqrt{\mathrm{10}}}{\mathrm{3}}\:=\:\frac{\mathrm{10}}{\mathrm{3}}\left(\mathrm{7}−\mathrm{2}\sqrt{\mathrm{10}}\right) \\ $$$$\:\:{G}\left[\frac{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{10}}}{\mathrm{3}}\:,\:\frac{\mathrm{10}}{\mathrm{3}}\left(\mathrm{7}−\mathrm{2}\sqrt{\mathrm{10}}\:\right)\right]\:. \\ $$
