Question Number 125384 by ajfour last updated on 10/Dec/20
Commented by ajfour last updated on 10/Dec/20

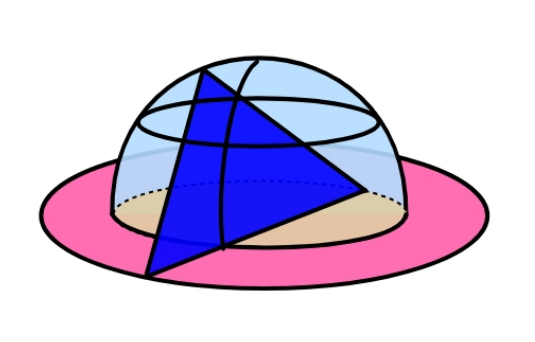
$${The}\:{hemisphere}\:{has}\:{radius}\:\mathrm{2}. \\ $$$${The}\:{outer}\:{circular}\:{base}\:{has}\:{radius} \\ $$$$\mathrm{3}.\:{Find}\:{maximum}\:{side}\:{length}\:{of} \\ $$$${equilateral}\:{triangle}\:{with}\:{vertices} \\ $$$${placed}\:{as}\:{shown}. \\ $$
Answered by mr W last updated on 10/Dec/20
Commented by mr W last updated on 10/Dec/20

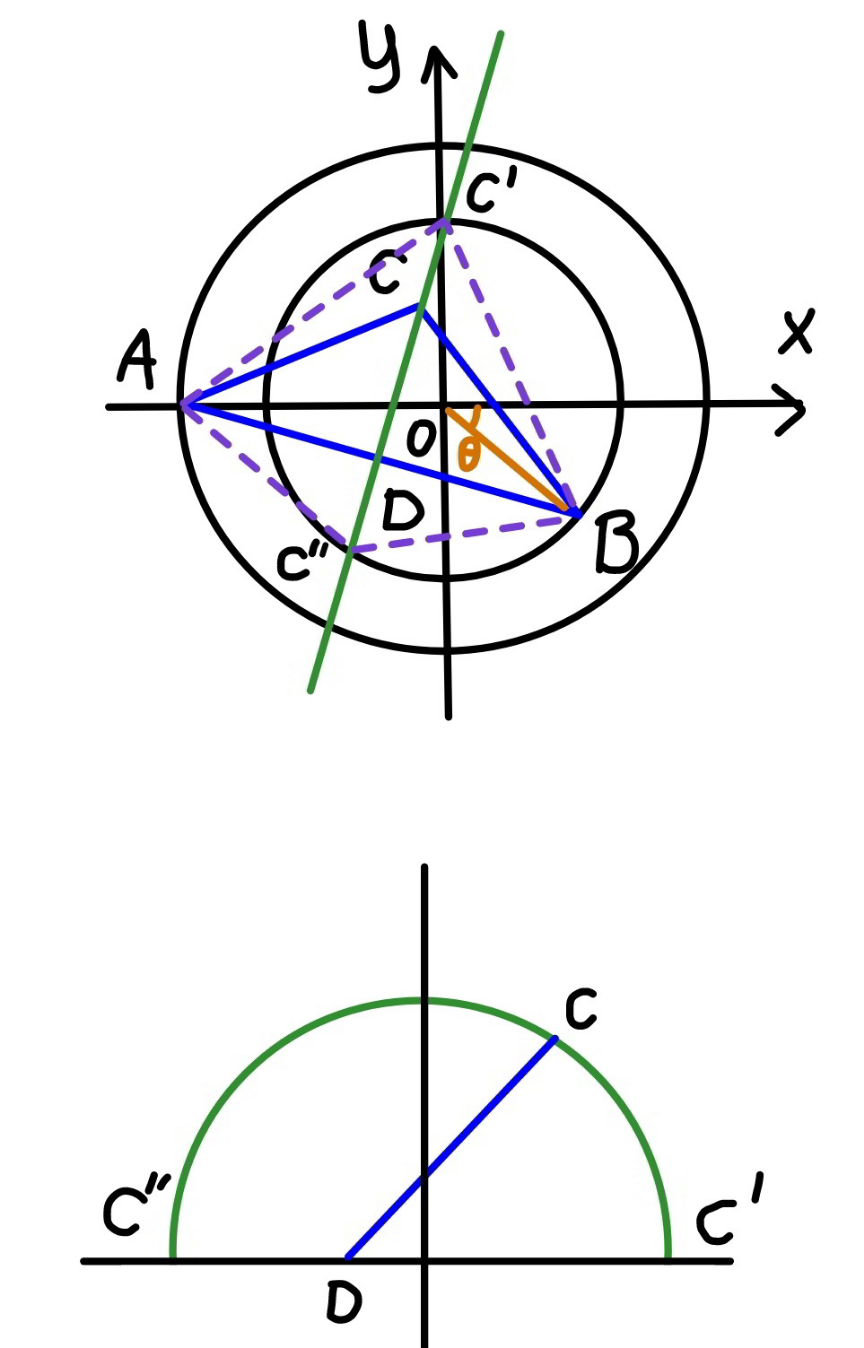
$${AB}={s} \\ $$$${DC}=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}} \\ $$$${DC}''\leqslant{DC}\leqslant{DC}' \\ $$$${that}\:{means}\:{the}\:{maximum}\:{equilateral} \\ $$$$\Delta{ABC}\:{is}\:\Delta{ABC}',\:{i}.{e}.\:{point}\:{C}\:{lies}\:{also} \\ $$$${on}\:{the}\:{base}. \\ $$
Commented by mr W last updated on 10/Dec/20

Commented by mr W last updated on 10/Dec/20
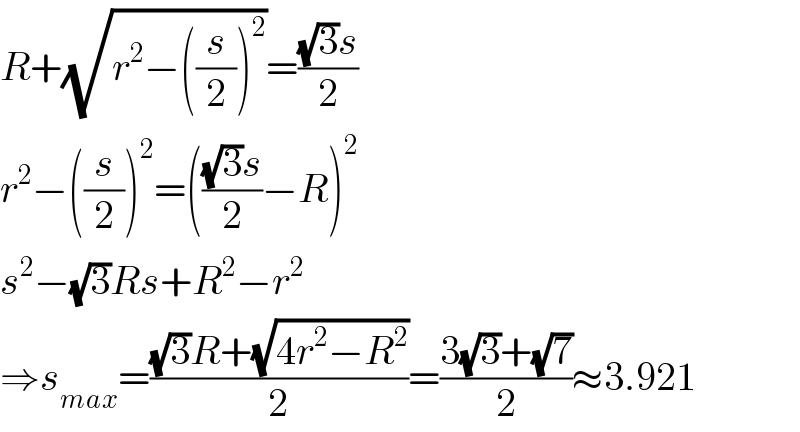
$${R}+\sqrt{{r}^{\mathrm{2}} −\left(\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} −\left(\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}−{R}\right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} −\sqrt{\mathrm{3}}{Rs}+{R}^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$$\Rightarrow{s}_{{max}} =\frac{\sqrt{\mathrm{3}}{R}+\sqrt{\mathrm{4}{r}^{\mathrm{2}} −{R}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\mathrm{3}\sqrt{\mathrm{3}}+\sqrt{\mathrm{7}}}{\mathrm{2}}\approx\mathrm{3}.\mathrm{921} \\ $$
Commented by ajfour last updated on 11/Dec/20
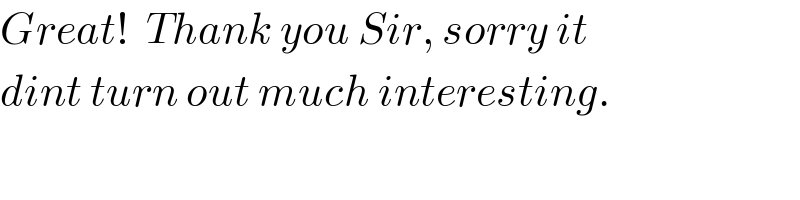
$${Great}!\:\:{Thank}\:{you}\:{Sir},\:{sorry}\:{it} \\ $$$${dint}\:{turn}\:{out}\:{much}\:{interesting}. \\ $$
